2.4. Проверочный расчет передачи

Условие контактной прочности [1, с. 15]:

,

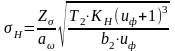где Z=8400 для косозубой передачи [1, с. 15];

К_н – коэффициент контактной нагрузки.

Коэффициент контактной нагрузки [1, с. 12]:

,

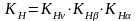где К_Н - коэффициент распределения нагрузки между зубьями [1, с. 15];

К_Н - коэффициент, учитывающий неравномерность распределения нагрузки по длине контактных линий [1, с. 15];

К_Нv – коэффициент, учитывающий внутреннюю динамику нагружения; [1, табл. 10.1].

где А=0,15 для косозубых передач [1, с. 15];

К_w – коэффициент, учитывающий приработку зубьев.

При НВ350 [1, с. 15]:

,

где V – окружная скорость в зацеплении.

тогда

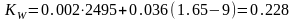
где 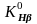- коэффициент неравномерности распределения нагрузки в начальный период работы. Для его определения найдем коэффициент ширины венца по диаметру [1, с. 15]:

Тогда [1, табл. 9.1]

МПа, что меньше расчетного _НР =509МПа. Недогрузка по контактным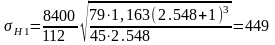 напряжениям 11%, что меньше допускаемых 15%.

Условие изгибной прочности

В зубьях шестерни [1, с. 16]:

,

В зубьях колеса [1, с. 16]:

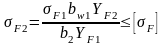
где Y_FS – коэффициент формы зубы [1, с. 17];

К_F – коэффициент нагрузки при расчете по напряжениям изгиба [1, с. 18];

Y_ - коэффициент, учитывающий угол наклона зуба в косозубой передаче [1, с. 16];

Y_ - коэффициент, учитывающий перекрытие зубьев [1, с. 16].

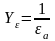
где _а – коэффициент торцевого перекрытия [1, с. 17].

,

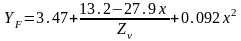где Z_v – эквивалентное число зубьев [1, с. 17], ;

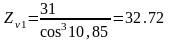
Коэффициент нагрузки

,

где К_F - коэффициент, учитывающий влияние погрешностей изготовления колес на распределение нагрузки между зубьями [1, с. 18];

К_F - коэффициент, учитывающий неравномерность распределения напряжений у основания зубьев по ширине зубчатого венца [1, с. 18];

К_Fv– коэффициент, учитывающий внутреннюю динамику нагружения [1, с. 18];

Недогрузка по контактным напряжениям не регламентируется.

Условия изгибной прочности передачи выполняются, поскольку _F1 [_FP1] и _F2 [_FP2].

Силы в зацеплении:

Окружная [1, с. 18]:

Радиальная [1, с. 18]

_,

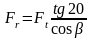Осевая [1, с. 18]:

3. Расчет плоскоременной передачи

Исходные данные

Крутящий момент на ведущем шкиве Т₁ = 43 Нм

Частота вращения ведущего шкива n₁= 960 об/мин

Передаточное число u=1,92

Относительное скольжение 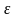= 0.015

Угол наклона передачи к горизонту 0

Тип нагрузки - средняяя

Число смен работы передачи в течение суток n_c=3.

1. Диаметры шкивов

Диаметр ведущего шкива определим из условия долговечности проектируемых кордшнуровых ремней [3. табл. 5.1.]. Примем d₁=180 мм, толщину ремня =2.8 мм.

Диаметр ведомого шкива равен:

d₂=u d₁=1,92(1-0,01)180=338,7 мм.

После округления получим: d₂= 355 мм.

2. Фактическое передаточное число

u_ф=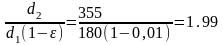

3. Предварительное значение межосевого расстояния

1,5 (d₁+d₂)=1,5(355+180)=802 мм.

4. Расчетная длина ремня

L=2 +0.5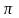 (d₁+d₂)+ =

Округлим до ближайшего числа из ряда:

L= 2500 мм.

После выбора L уточняем межосевое расстояние

= 0.125(2L-2W+ )=0,125(22500-2840+

+

где W = 0.5 (d₁+d₂)=0,53,14(180+355)=840 мм

Y = 2 (d₂-d₁)²=2(355-180)²=61250 мм²

5. Угол обхвата на ведущем шкиве

= -57 =

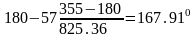
6. Скорость ремня

V = =

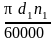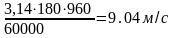
7. Окружное усилие равно

F_t = =

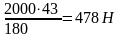
8. Частота пробегов ремня

= =

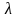9. Допускаемая удельная окружная сила:

,

где к₀ – допускаемая приведенная удельная окружная сила. к₀=1,6 МПа [3, табл. 5.1];

С – поправочные коэффициенты.

С_р=0,8; С_α=0,968 ; С_v=1; С_=1; С_d=1,2; С_F=0,85[3, табл. 5.2].

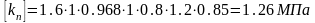
10. Ширина ремня:

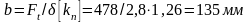
11. Площадь поперченного сечения ремня:

12. Сила предварительного натяжения ремня:

F₀ =A₀

где ₀ – предварительное натяжение, ₀ =2МПа [3, табл. 5.1]

F₀=3782=756 H

13. Силы натяжения ветвей ремня:

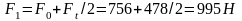
14. Сила давление ремня на вал:

F_оп= 2F₀ sin =2756sin(167.91/2)=1504Н

15. Проверочный расчет:

Максимальные напряжения в сечении ведущей ветви:

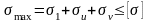
где ₁ – напряжение растяжения:

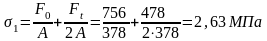
_и – напряжение изгиба:

_v – напряжение от центробежных сил:

,

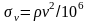где  - плотность материала ремня:  =1100 кг/м³ [3, с.81]

для плоских ремней.