8.Однофакторный дисперсионный анализ.

Основной задачей дисперсионного анализа является выявление фактора влияния одного или нескольких факторов на показатель У. Пусть изучается влияние фатора х на показатель у. Для этого фиксируются рез-ты измерений показателя у в различных группах. Пусть для каждого фактора х выделяют m уровней и для каждого уровня проведено n измер. В качестве нулевой гипотезы выдвигается предположение о том, что показатель у не зависит от фактора х. В этом случае необходимо сравнить разброс значений результатов измерений у относительно средних значений в каждой группе, а также относительно общего среднего. Если эти отклонения не существенны, то нулевая гипотеза о равенстве мат ожиданий принимается: . Это означает, что результаты измерений не отличаются друг от друга и поэтому их можно объединить в одну однородную группу. Это означает, что фактор х не влияет на показатель у. Результаты измерения показателя у можно занести в след таблицу:

№ измерения	Группы (уровни)
	1	2	…	j	…	m
1	Y11	Y12	…	Y1j	…	Y1m
2	Y21	Y22	…	Y2j	…	Y2m
…	…	…	…	…	…	…
i	Yi1	Yi2	…	yij	…	yim
….	…	…	…	…	…	…
n	Yn1	Yn2	…	ynj	…	ynm
Ср. в гр.
общ. Ср.

Среднее значение в каждой группе определяется по формуле: .

общее среднее: Н0=у1 среднее=у2 среднее=….ymсреднее.

Разброс средних значений по группе результатов измерений и общего среднего можно оценить с помощью следующей формулы: Q=Q1+Q2, где Q- сумма квадратов отклонений результатов измерений от общего среднего,т.е. Q=

Q1= илиQ1=n*

Q2=

На самом деле, Q=Q1+Q2+Q3, но Q3=0. поэтому Q=Q1+Q2 где Q1 называется межгрупповой разброс средних значений. Q2 харктеризует разброс средних результатов значений У относительно среднего значения и называется внутригрупповым рассеиванием.

Число степеней свободы : Q1: Q2:

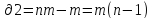
Для оценки дисперсии обозначим:

-Межгрупповая дисперсия:

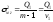
-Внутригрупповая дисперсия:

Для проверки нулевой гипотезы Но можно использовать отношение 2-х дисперсий : (эта величина подчиняется з-ну распределения Фишера)

F параметр- Критерий Фишера. Обозначим все возможные значения F через f . Закон распределения Фишера: Вся область всевозможных параметров f делится на 2-е части: РИСУНОК РАСПРЕДЕЛЕНИЯ ФИШЕРА!!!!

1) Область допустимых значений, куда значения параметра f попадают с большей вероятностью >90%

2) Область критических значений: p+q=1 p-попадающие в 90% q-не попадающие.

Вероятность попадания расчётного значения в критическую область назыв. уравнением значимости критерия фишера. Если Fрасч<Fкрит, то расчётное значение попадает в первую область допустимых значений , т.е. принимается нулевая гипотеза о равенстве математических ожиданий, и считается, что фактор х не влияет на у.Если наоборот, то для уровня значимости q расчетные значения критерия Фишера F попадают во II область и поэтому Н0 отвергается и принимается решение о том, что фактор х влияет на показатель у.