3.9. Коэффициент эластичности, бета-коэффициент и дельта-коэффициент для линейного уравнения регрессии

(3.45)

- номер опыта;

j - номер объясняющей переменной;

Коэффициент эластичности показывает: на сколько единиц (либо процентов) в долях от среднего значения измениться выходная величина , если объясняющая переменная х_j измениться на одну единицу (либо процент) в долях от среднего значения .

Таким образом, Э_j измеряет чувствительность к вариации х_j.

Замечание. В учебниках по эконометрике почему-то умалчивается вопрос: в долях от чего измеряются вариации и х_j? Без этой информации определения для Э_j становиться для студентов малопонятным.

Бета-коэффициент выражается формулой

(3.46)

Это – коэффициент отличается от коэффициента эластичности только масштабами нормировки х_j и : вместо средних взяты их средние квадратические отклонения.

– коэффициент показывает: на сколько % в долях от S_y измениться , если х_j измениться на 1% в долях от .

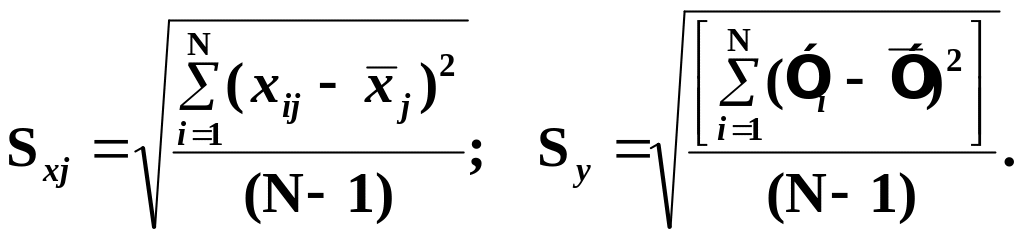(3.47)

Дельта-коэффициент определяется по формуле

(3.48)

Здесь – коэффициент парной корреляции между j-м фактором и зависимой переменой Y.

Дельта-коэффициент показывает долю влияния каждого фактора в суммарном влиянии всех факторов на зависимую переменную Y.

Глава IV. Временные ряды

4.1. .

Последовательность наблюдений моделируемого показателя, упорядоченная в порядке возрастания времени называется временным рядом (ВР):

У_t, t=t₁,t₂,…,t_i,…,t_n;

t_i>t_i-1.

Обычно в экономических задачах временной интервал отсчетов постоянен (t=const). Тогда можно указывать просто номер отсчета.

У_t, i=1,2,...,N.

Замечание:

1). Уровни временных рядов У_t не являются взаимно независимыми, как того требует первая предпосылка метода наименьших квадратов. Поэтому разработаны специальные методы оценки параметров уравнения регрессии. В этом отличие временных рядов от базы данных пространственного типа.

4.2. Компонентный анализ временных рядов

У_t=U_t+ V_t+ C_t+ E_t, t=1,2, (4.1)

4.3. Понятие случайного процесса

Стационарные временные ряды

Случайный процесс (или случайная функция) неслучайного аргумента t – называется функция, которая при любом t является случайной величиной.

Определение 1: Y_t называется строго стационарным (стационарным в узком смысле), если в различных временных срезах t=var выполнено два условия:

1. Вид закона распределения свободных величин Y один и тот же (например – нормальный закон распределения остатков);

2. Числовые параметры закона распределения (числовые характеристики) одинаковы:

M(Y(t))=a=const; D[Y(t]= ²= const.

Определение 2: Если выполнено только условие № 2 то временные ряды называются стационарными в широком смысле или эргодическим. Другими словами эргодический случайный процесс протекает однородно по времени.

Замечание: В дисциплине «Теория вероятности и математическая статистика» показано что «Выборочные оценки вероятностных характеристик эргодического процесса могут быть вычислены по одной фиксированной реализации для наблюдений в разные моменты У_t, р=const.

(4.2)

Пример:

Стационарного случайного процесса – «белый шум», т.е. возмущения E_i при условии:

M[E_i]=0

M[E_i E_k]=0 – отсутствие корреляции.

Если EN(0;_E²), то шум нормальный (гауссовский) белый.