3.5. Свойства оценок, получаемых по методу наименьших квадратов

Утверждение: Оценка по методу наименьших квадратов при выполнении предпосылок метода наименьших квадратов обладает важными статистическими свойствами:

1). Она несмещенная (не содержит систематических ошибок)

(Mb_j= _j), j= . (3.15)

2). Оценка метода наименьших квадратов – состоятельная

(3.16)

Здесь  - сколько угодно малое число.

Другими словами, при увеличении N оценка вектора становиться все более точной, приближаясь к генеральному значению по вероятности.

Заметим, что без этого свойства организация эксперимента была бы затруднительной.

3). Эффективность оценки (теорема Гаусса-Маркова).

Если уравнение регрессии – это классическое нормальное линейное регрессии, т.е. удовлетворяются все предпосылки регрессионного анализа, то в классе линейных несмещенных оценок метода наименьших квадратов – оценка является наиболее эффективной, т.е. обладает наименьшей дисперсией.

3.6. Оценка адекватности уравнения регрессии (проверка гипотез о предпосылках метода наименьших квадратов)

3.6.1.Гипотеза о близости к нулю математического ожидания остатков

Здесь используется критерий Стьюдента для остатков и проверяется нуль-гипотеза:

(3.17)

S_ - среднее квадратичное отклонение остатков – мера рассеяния остатков относительно своего среднего

(3.18)

Замечание: Здесь число степеней свободы S_=(N – 1), так как на вычисление среднего (центра рассеяния) расходуется одна степень свободы:

(3.19)

где S_e- среднее квадратичное отклонение наблюдений Y_i относительно поверхности регрессии :

(3.20)

где, k – число членов уравнения регрессии, включая свободный член.

3.6.2. Гипотеза о статистической значимости коэффициентов регрессии bj

Используя t – критерий Стьюдента проверяем нуль гипотезу:

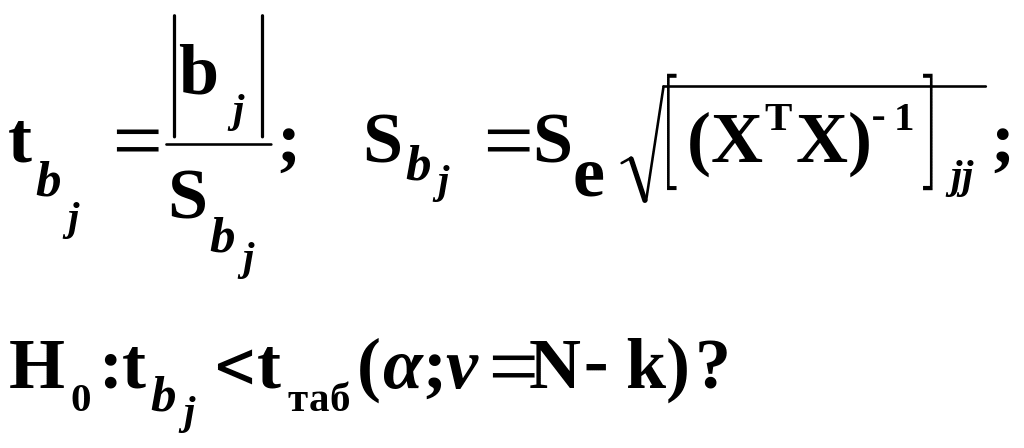(3.21)

Выводы:

• Если данное неравенство выполнено, то коэффициент b_j – статистически не значим.

• Если все коэффициенты в уравнение регрессии не значимы то уравнение регрессии не значимо: влияние регрессоров Х_j на формирование значений Y не различимо на фоне случайных возмущений E. Модель не адекватна.

• Если все коэффициенты уравнения регрессии значимы, то нарушение адекватности в данном пункте (по данной гипотезе) нет. Но вывод об адекватности делать рано, должны быть выполнены все предпосылки метода наименьших квадратов.

• Если часть коэффициентов уравнения регрессии значима, а часть не значима, то это не является снованием для нарушения адекватности. Значимая часть регрессоров может адекватно описывать объект.

• Незначимые коэффициенты уравнения регрессии и соответствующие им регрессоры следует исключить из модели: они не несут никакой полезной информации.

3.6.3. Гипотеза о статистической значимости всего уравнения регрессии в целом

Используется критерий Фишера- Снедекора F и проверяется нуль-гипотеза:

(3.22)

Q_R – сумма квадратов отклонений расчетных значений от среднего , обусловленная вариацией факторов; Q_e - сумма квадратов отклонений расчетных значений от фактически наблюдаемых, обусловленная влиянием случайных возмущений E_i (включая влияние неучтенных в модели факторов).

Выводы:

1. Если гипотеза Н₀ выполнена, то уравнение регрессии в целом статистически незначимо и можно сразу делать вывод о неадекватности модели.

2. Если нуль-гипотеза Н₀ не выполнена, т.е. F>F_таб, то уравнение регрессии в целом значимо и можно переходить к проверке других гипотез.