21. При соедин. Звездой концы фаз соед.В 1 точку,которую назыв. Нулевой

или нейтральной.Провод,соединяющий нулевые точки источника и приемника

назыв.нулевым или нейтральным.В соотв.с этим различают трехпроводную

(без нейтрали)и четырехпроводную(с нейтралью) схемы соедин.Провода,соединяющ.

источник и фазы нагрузки назыв.линейными проводами.Линейные токи-токи,проходящие

по линейным проводам.Фазные токи-токи в фазах источника и приемника.При соединен. звездой

линейные и фазные токи одинаковы.Фазное напр.-разность потенциалов

между линейными зажимами и нейтралью.Линейное напр.-разность потенциалов между

каждой парой линейных проводов.При соединении звездой линейные напряжения связаны

с фазными напряжениями в соотношении {(система)Uab=Ua-Ub;Ubc=Ub-Uc;Uac=Ua-Uc. Могут

быть построены векторные диаграммы.На топографической векторной диаграмме каждой

точке цепи соотв.точка на диаграмме. Ua=√3*Uф

22.При соединении тр-ком конец предыдущей фазы соедин. с началом следущей,

при этом образуется замкнутый контур.При отсутствии нагрузки ток в контуре равен 0.

Если к узловым точкам А^, B^, C^, применить 1й з-н Кирхгофа,то получится соотношение

между линейными и фазными токами {Ia=Iab-Ica;Ib=Ibc-Iab;Ic=Ica-Icb. Могут быть

построены диаграммы: полярная,топографическая. I_u=√3*I_ф

23. Сделаем упрощение:сопр.линейных проводов и фаз источкина будем полагать

равным 0.Схема представляет собой эл.цепь с двумя узлами.Ее удобно рассчитывать

методом узлового напр.1.Опред.напряж. между нулевыми точками N и N^, :

Un=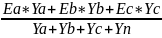 .2.Опред.напр.на фазах приемника: U_(a,b,c) =E_(a,b,c)-U_n.3.Опред.

фазные токи: I_(a,b,c)=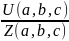 .4.Опред.ток в нулевом проводе: In=Un/Zn ; In=Ia+Ib+Ic

.Топограф.диаграмма цепи при несимметрич. нагрузке.При наличии

сопротивл. в нулевом проводе нулевая точка приемника не совпадает с нулевой

точкой источн.Напряж. на фазах приемника оказыв. неодинаков. возникает напряж.

смещ. нейтрали.

24.Символич.метод расчета: U_л=U_ф U_AB = U_ф U_BC =U_ф e^–j120 U_CA = U_ф e^j120 1.Опред.сопр.

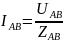
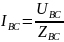
фаз. Z_AB, Z_BC , Z_CA 2.Опред.фазные токи. 3.Опред.

линейные токи. I_A=I_AB-I_CA I_B=I_BC-I_AB I_C=I_CA-I_BC Векторная диаграмма строится на компл.

форме.Графо-аналитич.метод:1.Опред.сопр.в каждой фазе. 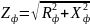X_ф=Х_L-X

_c 2.Опред.фазные токи.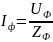 3.Опред.линейные токи по векторн. диаграмме построив

их исходя из соотнош.(под сист.) .

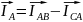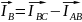
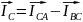
4.Строим векторную диаграмму. Мощности при соедин. в треуг. определ.аналогично мощн. при

соедин. звездой.

25. В символич.форме: S=Sa+Sb+Sc=Pa±jQa+Pb±jQb+Pc±jQc=(Pa+Pb+Pc) ±j(Qa+Qb+Qc)=P±jQ.

S_A =U_A*I_A =R_A±jQ_A S_B =U_B*I_B =R_B±jQ_B S_C =U_C*I_C =R_C±jQ_C . Аналитич.метод расчета: Активная

мощность фаз и цепи: P_(a,b,c) =U_(a,b,c) *I_(a,b,c) *cosφ_(a,b,c) ; P=Pa+Pb+Pc. Реактивная мощность фаз

и цепи: Q_(a,b,c) =U_(a,b,c) *I_(a,b,c) *sinφ_(a,b,c) ; Q=Qa+Qb+Qc. Для каждой фазы может

быть определена полная мощность: S_(a,b,c) =U_(a,b,c) *I_(a,b,c) ; S=√P² +Q²

26. Рассмотрим одну фазу 3-х фазной обмотки. Ее проводники распр. Равномерно на 1/3

части внутренней поверхности статора. Плоскость перпендик. оси магн. потока которой

статор и ротор делятся на две части наз. нейтралью.На одной их них нах. северный

полюс а на другой южный. Рассмотрим так же развертку статора. Однофазная обмотка

образует одну пару магнитных полюсов а график распр. магнитной индукции представляет

сабой равнобокую трапецию. По форме такой график близок к синусойде поэтому для

упрщения расчетов заменим действит. график синусоид. кривой с амплитудой В_м уравн.

которой В=В_м*cosβ где β-это угол по окр. статора отсчитанный под оси А в положительн.

направл. При пост. токе такое распр магн индукции в доль возд. зазора сохр пока имеется

ток в катушке . При переменном токе в катушке в любой момент времени простр распр

магн индукции остается синусоидальным но в каждой точке возд зазора велечина ее

изменяется с течением времени.Магн. поле в этом случаи называется пульсирующим в

возд. зазоре образ. стоячая волна магн. индукцмм.. Уравнения магн индукции пульс поля

B= Bm sinwt cosB. Пульсируюшее магн поле можно разложить на два круговых вращающихся

в противополжные стороны с одинаковой скоростью.Скорость вращ.магн. поля обратно

прапорц. числу пар полюсов образ. обмоткой с током.

27. Токи в катушках определяют с учетом временного сдвига на 90 эл гр. Ia=Im sinwt Ib=Im sin(wt – П/2)

. Магнитная индукции для фазы А

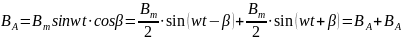
Для фазы В 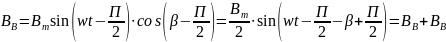Сумма составл.

вращ. против. положит. напряж. отсчета угла :

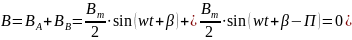
Сумма составл. вращ. в прямом направл. равна индукции результ. поля 2ф обмотки

Двухфазная система

обмоток имеющая пространственный сдвиг фаз на 90 эл гр при временном сдвиге токов в них на

такой же угол создает вращающееся круговое магн. поле.

28. Токи в катушках измен. согласно уравн.Ia= Im sinwt Ib=Im sin( wt-120) Ic= Im sin ( wt+ 120).

Магнитное индукция результирующего поля B= Ba +Bb + Bc. При симметричном расположении

трехфазной обмотки отн окружности статора и при симметричной системе токов в ней,

магнитное поле круговое . При прямой последовательности токов в фазах максимумы

их поступают в порядке A B C .Если на статоре обм фаз расположены так что обход их в

указаном порядке совершается в направлении движения часовой стрелки то и поле

вращается в ту же сторону. При обратной последовательности токов в фазах A C B то

при прежнем расположении обмоток поле вращается против часовой стрелки