20. Системы счисления, используемые в компьютерах и алгоритмы приеобразования из одной сс в другую

Системой счисления называется способ представления (кодирования) чисел посредством некоторого множества символов, называемых цифрами.

В любой системе счисления число может быть записано в виде некоторой строчки символов:

а_nа_n-1а_n-2…а₁a₀,a_-1a_-2a_-3…a_-m

где a_i – символы из некоторого множества {a}, ‘,’ – запятая, отделяющая целую часть числа от дробной части.

Система счисления называется позиционной, если значение символа (цифры) определяется не только видом, но и местом расположения (позицией) в представлении числа.

Непозиционными называются системы счисления, где символы, из которых состоит представление числа, не имеют самостоятельного значения, а имеют смысл только взятые в совокупности (например, коды Грея, Джонсона и др.).

Любое число в позиционной системе счисления может быть представлено в виде:

a_n·qⁿ + a_n-1·q^n-1 + … + a₁·q¹ + a₀·q⁰ + a_-1·q^-1 + a_-2·q^-2 +…+ a_-m·q^-m

где: a_i – цифра числа;

i – позиция цифры (отрицательные позиции определяют позиции

дробной части числа).

q – основание позиционной системы счисления.

В вычислительной технике используются следующие системы счисления.

1. Двоичная:

q = 2; {a} → 0,1;

Представление числа в двоичной системе счисления обычно обозначается символом B (Binary), например, 101011B.

2. Восьмеричная:

q = 8; {a} → 0,1,2,3,4,5,6,7;

Представление числа в восьмеричной системе счисления обозначается символом O (Octonory) или Q, например.

3. Десятичная:

q = 10; {a} → 0,1,2,3,4,5,6,7,8,9;

Представление числа в дес. CC либо подразумевается по умолчанию, либо обозначается символом D (Decimal).

4. Шестнадцатеричная:

q = 16; {a} → 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F;

Представление числа в шестнадцатеричной системе счисления обозначается символом H (Hexadecimal).

5. Двоично-десятичная:

q = 10; {a} → 0,1,2,3,4,5,6,7,8,9;

но a_i – кодируется четырьмя двоичными разрядами.

Поскольку четырьмя двоичными разрядами можно закодировать до 16 символов, а кодируется только 10, то разновидностей двоично-десятичных кодов может быть много, в зависимости от весовых значений позиций этого четырехразрядного двоичного числа. В вычислительной технике наиболее широко используется двоично-десятичный код с весовыми значениями разрядов, соответствующими числам 8421. Поэтому для этого двоично-десятичного кода:

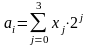где x_i = {0,1}; и ;

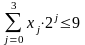Представление числа в двоично-десятичной системе счисления обозначается символами BCD (Binary Code Decimal).

Заметим, что при ручной записи на бумаге, систему счисления, в которой представлено число, бывает удобнее указывать в виде индекса после младшего разряда числа, например:

1011101₂ ; 101245₈ ; 23456₁₀ ; 7F5AC₁₆ ; 100101111000_2/10,

где индекс 2/10 указывает на двоично-десятичную систему счисления, в которой представлено число.

При изложении правил перевода представления чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную рассмотрим только те алгоритмы, в которых все требуемые арифметические вычисления осуществляются в десятичной системе счисления. В этом случае целая часть десятичного числа и дробная его часть преобразовываются по различным алгоритмам.

При преобразовании целого числа или целой части вещественного числа в другую позиционную систему счисления, алгоритм преобразования заключается в последовательном делении этого числа на основание искомой системы счисления. Остатки от этого последовательного деления образуют последовательность цифр в искомой системе счисления. При этом, последний остаток будет являться первой цифрой искомого числа в требуемой системе счисления, а первый – последней.

Преобразование дробной части десятичного числа в дробную часть двоичного, восьмеричного или шестнадцатеричного числа осуществляется путем последовательного умножения этой дробной части на основание искомой системы счисления и выявлении получающейся целой части, при каждом умножении. Эти появляющиеся целые части будут являться цифрами целой части искомого числа в требуемой системе счисления. При этом цифры разрядов будут получаться в прямом порядке (цифрой старшего разряда дробной части числа является первая, полученная после умножения целая часть). Окончание преобразования дробной части числа определяется появлением всех нулей в разрядах, отводимых под дробную часть. Если же такое последовательное умножение до получения нулей в дробной части произведения продолжается очень долго, то, в таких случаях преобразование дробной части числа осуществляется до требующейся погрешности (числа знаков в дробной части).