Найдем Dmax для случая отсутствия связанных рангов (все объекты различны), предварительно показав, что d зависит только от n и m (числа объектов и количества экспертов). Подставив (1) в (3), получим

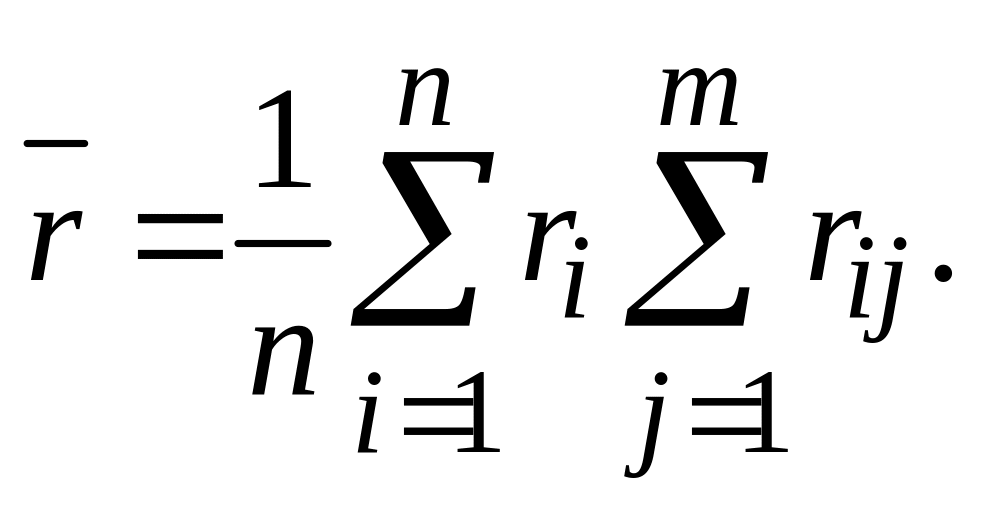(5)

Если j = const, найдем сумму рангов для j-го эксперта. Поскольку для ранжирования используются натуральные числа от 1 до n, можно записать сумму натуральных чисел от 1 до n:

(6)

Подставив (6) в (5), получим:

(7)

Из (7) видно, что величина зависит только от n и m (числа объектов и количества экспертов). Осуществив ряд последовательных преобразований [9], можно получить

Введя обозначение можно записать выражение для оценки D в виде

Тогда окончательное выражение для коэффициента конкордации (для случая отсутствия связи рангов) запишется как

(8)

максимальное значение дисперсии достигается в случае полного совпадения мнений экспертов. Минимальное значение дисперсии, которое равно нулю, достигается в случае, если эксперты дают несовпадающие мнения. Доказательство этого утверждения здесь не приводится, оно дано в [9]. При наличии связанных рангов коэффициент конкордации вычисляется по формуле

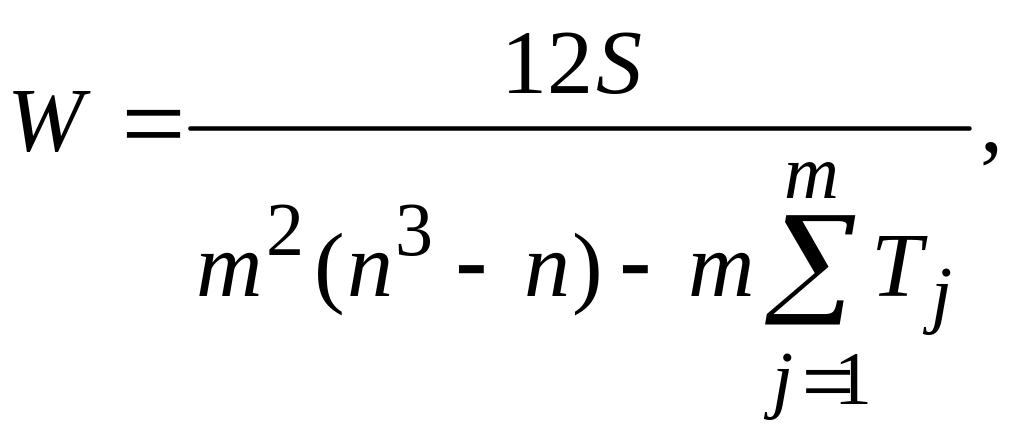
где Здесь Т_j – показатель связанных рангов в j-й ранжировке, H_j – число групп равных рангов в j-й ранжировке, h_k – число равных рангов в k-й группе связанных рангов в ранжировке j-го эксперта.

ДКК = 1, если все ранжировки одинаковы (имеется явный сговор [7]).

ДКК = 0, если все ранжировки различны (некомпетентность [7]).

ДКК можно считать случайной величиной. В таком случае необходимо дать оценку значимости значения ДКК. Для больших значений n и m (при n > 7) можно использовать критерий .

Доказано, что величина w = m(n – 1) имеет распределение с степенями свободы.

При наличии связанных рангов (более общего случая)

Определение взаимосвязи ранжировок. Для решения задачи определения зависимости между ранжировками двух экспертов или связи между достижением двух различных целей при решении одной и той же совокупности проблем или взаимосвязи между двумя признаками используют меру, называемую коэффициентом ранговой корреляции (КРК).

Характеристикой взаимосвязи множества ранжировок или целей будет являться матрица КРК. Известны КРК Спирмена и Кендалла.

КРК Спирмена определяется формулой

где К₁₂ – взаимный корреляционный момент первой и второй ранжировок, D₁, D₂ – дисперсии этих ранжировок. Для определения взаимовлияния двух ранжировок К₁₂ , D₁ и D₂ вычисляются по формулам:

где n – число ранжируемых объектов; – ранги в первой и второй ранжировках соответственно; – оценки средних рангов.

Оценки средних рангов определяются как

Проведя ряд преобразований, можно получить удобную для расчетов формулу КРК Спирмена для несвязанных рангов:

КРК Спирмена изменяется от –1 до +1. КРК = 1 при одинаковых ранжировках, т.е. при . Значение  = –1 имеет место при противоположных ранжировках (прямой и обратной). Если КРК=1, то ранжировки считаются линейно независимыми.

Определить значимость случайной величины  можно с помощью следующих формул и рассуждений.

Если || < , где  – пороговое значение случайной величины  для вероятности , то оценка КРК Спирмена считается значимой.  определяется как

где n – количество объектов;

(х) – функция, обратная функции

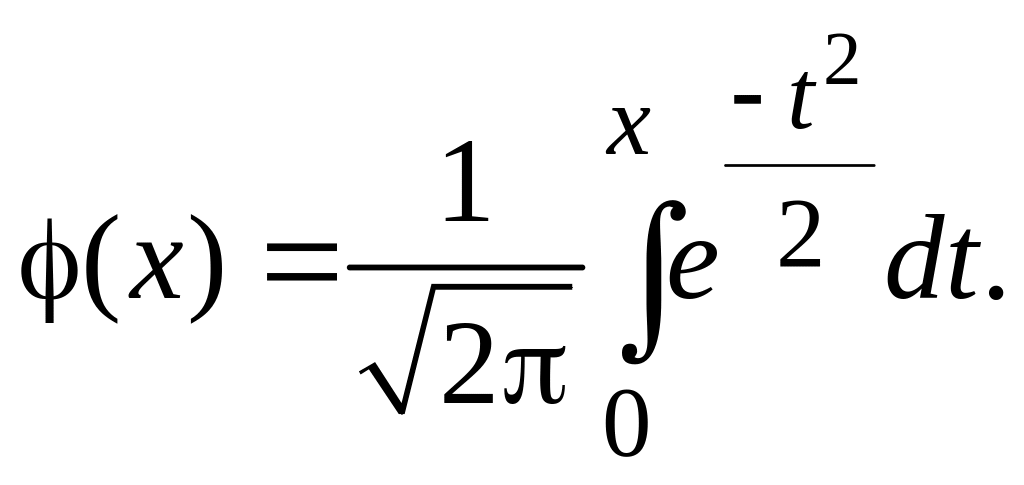
Значения функции табулированы [11].

Для определения значимости оценки КРК Спирмена можно воспользоваться критерием Стьюдента, поскольку величина приближенно распределена по закону Стьюдента с n – 2 степенями свободы.

Для связанных рангов КРК Спирмена имеет вид:

где  – оценка КРК Спирмена,

здесь k₁ и k₂ – количество связанных рангов в первой и второй ранжировках соответственно.

КРК Кендалла при отсутствии связанных рангов определяется формулой:

где n – количество объектов; r_ij – ранги объектов; sign х

.

Сравнение (из опыта использования) обоих КРК показывает, что КРК Спирмена дает более точный результат и рассчитывается по более простой формуле, т.е. при практических расчетах он более предпочтителен.

Пример. Два эксперта провели ранжирование пяти объектов. Результаты ранжировки приведены в таблице.

Оj Эi	О1	О2	О3	О4	О5
Э1	2	1	4	3	5
Э2	1	2	4	5	3
(r1j – r2j)	1	–1	0	–2	2
(r1j – r2j)2	1	1	0	4	4

КРК Спирмена .

Определим порог  при  = 0,05:

.

Поскольку  = 0,5 <  = 0,98, оценка КРК является значимой.

Энтропийный коэффициент конкордации (ЭКК) определяется формулой из [9]:

где Н – энтропия, вычисляемая как

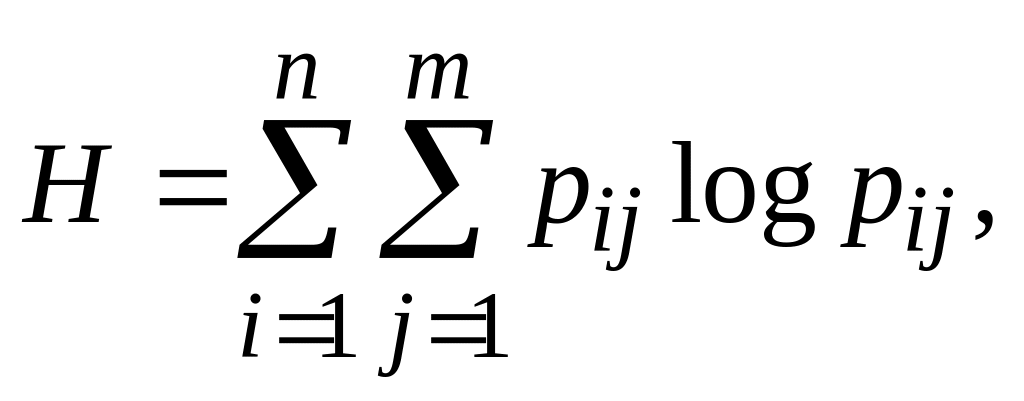
Н_max – максимальное значение энтропии, Р_ij – оценки вероятностей j-го ранга, присваиваемые i-му объекту; – отношение количества экспертов m_ij, приписавших объекту О_i ранг j, к общему числу объектов m.

Максимальное значение энтропии достигается при равновероятном распределении рангов, т. е. когда тогда Подставив Р_ij в выражение для определения Н, получим:

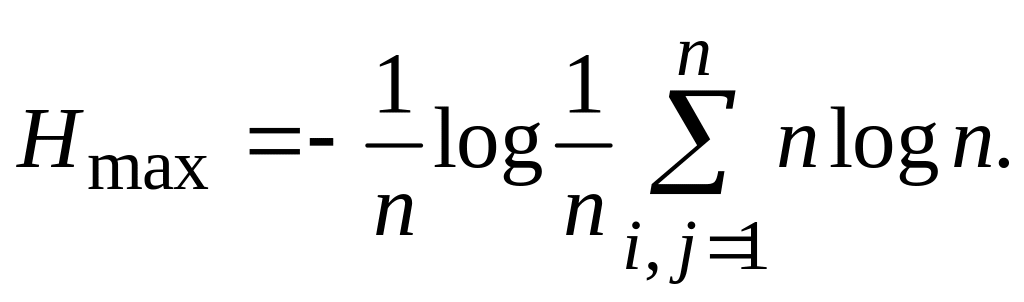
Значение ЭКК изменяется от нуля до единицы. При W_э = 0 расположение объектов по рангам равновероятно, поскольку Н = H_max. Данный случай может быть обусловлен либо невозможностью ранжировки объектов по заданным показателям, либо полной несогласованностью мнений экспертов. При W_э = 1 (при Н = 0) все эксперты дают одинаковую ранжировку.

ЭКК и ДКК дают примерно одинаковую оценку согласованности мнений экспертов при различных ранжировках. Но ЭКК позволяет обнаружить факт разделения мнений экспертов на две противоположные группы (в таком случае ЭКК = 0,7, а ДКК = 0). Однако объем вычислений для ЭКК несколько больше, чем для ДКК.

В настоящее время для сбора и обработки эвристической информации применяют новые теории, например, теорию нечетких множеств. В работе [17] приводятся примеры использования возможностей, параметрическое представление управленческих оценок в виде нечетких интервалов, сравнение нечетких интервалов и др.