9.3. Общий индекс как средняя величина индивидуальных индексов

Общий индекс можно получить как среднее значение соответствующих индивидуальных индексов. В этом смысле общим индексом отражаются результаты изменения уровня явления у отдельных единиц совокупности. При расчете общего индекса как средней величины веса индивидуальных индексов подбираются так, чтобы был возможен алгебраический переход от общего индекса в форме средней величины к общему индексу в агрегатной форме⁴. Эти преобразования, как правило, не сложны. Например, индекс общего объема товарооборота можно представить средней арифметической величиной -

.

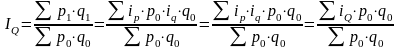Тот же индекс может быть записан в форме средней гармонической величины.

.

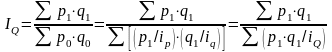Индекс изменения общей суммы товарооборота в связи с изменением количества проданных товаров (индекс физического объема – I_q) можно представить как

(В форме средней гармонической индекс физического объема практически не используется).

Индекс изменения общей суммы товарооборота в связи с изменением цен на товары (I_p) можно представить средней гармонической величиной:

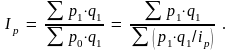
23.​ Индексы средних величин: индексы переменного, постоянного составов, влияние структурных сдвигов.

9.5. Индексы средних величин

Отношение средних величин называется в статистике индексом переменного состава. В индексе переменного состава учитывается одновременно и влияние структурных изменений в составе совокупности, и изменение уровня качественного признака у отдельных объектов. В этом смысле показанные ранее индексы, полученные по типу индекса цен, являются индексами постоянного, или фиксированного состава. Индекс переменного состава выражается произведением индекса структурных изменений на индекс постоянного состава:

I_{пер.сост} = I_стр ·I_{пост.сост} .

Представление индекса переменного состава произведением двух сопряженных индексов позволяет выяснить роль соответствующих факторов в изменении среднего уровня качественного показателя. Так, в примере, средний уровень процентной ставки (4,0994011 в базисном периоде; 3,927 в отчетном) изменился в форме индекса переменного состава в

I_{пер.сост} = 3,927/4,0994011 = 0,957945 раза.

За счет перераспределения суммы кредитов между их видами средний уровень процентной ставки изменился в I_стр=0,9310615 раза (индекс структурных изменений). За счет изменения процентной ставки по отдельным видам кредита средний размер этой ставки изменился в I_{пост.сост}=1,0288737 раза (индекс постоянного состава).

За счет перераспределения суммы кредитов между их видами средний уровень процентной ставки изменился в I_стр=0,9310615 раза (индекс структурных изменений). За счет изменения процентной ставки по отдельным видам кредита средний размер этой ставки изменился в I_{пост.сост}=1,0288737 раза (индекс постоянного состава).

Формулы расчета этих индексов показаны выше, именно эти индексы использовались при анализе изменения общей суммы дохода, полученного банком от предоставления кредитных услуг. Единственное замечание это то, что при расчете индекса постоянного состава можно использовать либо постоянный количественный состав совокупности, либо постоянный удельный вес каждой части совокупности в общем объеме количественного признака (в общей сумме кредитных услуг. Действительно,

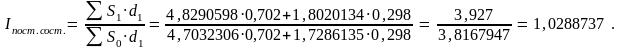
24.​ Основы индексного факторного анализа. Методы разложения абсолютного прироста по факторам.

 статистике, планировании и анализе хозяйственной деятельности основой для количественной оценки роли отдельных факторов в динамике изменений обобщающих показателей являются индексные модели. Индексный метод – один из приемов элиминирования. Основывается на относительных показателях динамики, пространственных сравнений, выполнении плана, выражающих отношение фактического уровня анализируемого показателя в отчетном периоде к его уровню в базисном периоде (или к плановому, или по другому объекту). Любой индекс исчисляется сопоставлением соизмеряемой (отчетной) величины с базисной. Индексы, выражающие соотношение непосредственно соизмеряемых величин, называются индивидуальными, а характеризующие соотношения сложных явлений – групповыми, или тотальными.

Статистика оперирует различными формами индексов (агрегатная, арифметическая, гармоническая и др.), используемыми в аналитической работе.

Агрегатный индекс является основной формой любого общего индекса; его можно преобразовать как в средний арифметический, так и в средний гармонический индексы. С помощью агрегатных индексов можно выявить влияние различных факторов на изменение уровня результативных показателей в мультипликативных и кратных моделях.

Корректность определения размера каждого фактора зависит от:

1. количества знаков после запятой (не менее четырех);

2. количества самих факторов (связь обратно пропорциональна).

Принципы построения индексов: изменение одного фактора при неизменном значении всех остальных, при этом если обобщающий экономический показатель представляет собой произведение количественного (объемного) и качественного показателей-факторов, то при определении влияния количественного фактора качественный показатель фиксируется на базисном уровне, а при определении влияния качественного фактора количественный показатель фиксируется на уровне отчетного периода.

Пусть Y = а*b*с*d. Тогда:

При этом: I Y=I a*I b*I c*I d.

Индексный метод позволяет провести разложение по факторам не только относительных, но и абсолютных отклонений обобщающего показателя. В этом случае влияние отдельных факторов определяется с помощью разности между числителем и знаменателем соответствующих индексов, т. е. также при расчете влияния одного фактора элиминируется влияние другого:

Пусть Y = а*b, где а – количественный фактор, a b – качественный. Тогда:

a 1*b 0—a 0*b 0– абсолютный прирост результирующего показателя за счет фактора а;

a 1*b 1—a 1*b 0– абсолютный прирост результирующего показателя за счет фактора b;

a 1*b 1—a 0*b 0– абсолютный прирост результирующего показателя за счет влияния всех факторов.

Данный принцип разложения абсолютного прироста (отклонения) обобщающего показателя по факторам пригоден для случая, когда число факторов равно двум (один из них количественный, другой – качественный), а анализируемый показатель представлен как их произведение.

Теория индексов не дает общего метода разложения абсолютных отклонений обобщающего показателя по факторам при числе факторов более двух. Для решения этой задачи используется метод цепных подстановок.

25.​ Территориальные индексы: понятие, способы расчета.