15.​ Ранговая корреляция, понятие, методы ее измерения.

8.      Метод ранговой корреляции Спирмена позволяет определить силу и направление корреляционной связи между двумя признаками или двумя иерархиями признаков.

 

Для подсчета ранговой корреляции необходимо располагать двумя рядами значений, которые могут быть проранжированы. Такими рядами могут быть:

 

А) Два признака, измеренные в одной и той же группе переменных (наиболее часто в этом качестве выступает группа людей, которых принято тогда именовать испытуемыми или респондентами. Естественно, под переменными подразумеваются не сами люди, а данные ими ответы на те или иные вопросы.)

Б) две индивидуальные иерархии признаков, выявленные у двух испытуемых по одному и тому же набору признаков (скажем, по ответам на пункты анкеты или теста).

В) Две групповые иерархии признаков (например, соответствие каких-либо выборов, сделанных одной группой людей выборам другой группы).

Г) Индивидуальная и групповая иерархии признаков (например, сопоставление индивидуальной иерархии жизненных ценностей сотрудника усредненному мнению группы на этот же счет; сопоставление последовательности товаров, которые приобрели бы (в среднем) жители города А и города Б при условии получения премии, на которую заранее не рассчитывали.)

 

9.      Ограничения метода ранговой корреляции. По каждой переменной должно быть представлено не менее 5 наблюдений. Верхняя граница  выборки – меньше или равна 40. Коэффициент ранговой корреляции Спирмена r_s при большом количестве одинаковых рангов по одной или обеим сопоставляемым переменным дает огрубленные значения. В идеале оба коррелируемых ряда должны представлять собой две последовательности несовпадающих значений. В случае несоблюдения такого условия вносится поправка на одинаковые ранги (будет дано ниже). Помимо этих ограничений, следует так же помнить об ограничениях корреляционного метода вообще – невозможность обнаружения причинной связи между явлениями.

16.​ Ряды динамики: понятие, виды, правила построения, элементарные показатели анализа.

Ряд динамики (хронологический, динамический, временной ряд) – представляет последовательность упорядоченных во времени числовых показателей, характеризующих уровень развития изучаемого явления. Любой ряд динамики включает, следовательно, два обязательных элемента: во-первых, время и, во-вторых, – конкретные значения показателя, или уровни ряда. Ряды динамики различаются по признакам

1. По времени – моментные и интервальные ряды. Интервальный ряд динамики – последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. Таковы, например, ряды показателей объема продукции по месяцам года, количества отработанных человеко-дней по отдельным периодам, объём реализации за период и т.д. Если же уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени, то совокупность уровней образует моментный ряд динамики. Примерами моментных рядов могут быть последовательности показателей численности населения на начало года, величины запаса какого-либо материала на начало периода и т.п. Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда дает вполне реальный показатель – общий выпуск продукции за год, общие затраты рабочего времени, общий объем продаж и т.д. Сумма же уровней моментного ряда обычно не имеет реального содержания (хотя иногда и подсчитывается).

2. По форме представления уровней – ряды абсолютных, относительных и средних величин.

3. По расстоянию или интервалам времени между датами выделяют полные (равноотстоящие) и неполные хронологические ряды.

В полных рядах динамики даты регистрации или моменты времени следуют друг за другом через равные интервалы. Неполные – когда принцип равных интервалов не соблюдается.

4. По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики. Если ведется анализ во времени одного показателя, имеем изолированный ряд динамики (табл. 8.1 и 8.2). Комплексный ряд динамики, когда в хронологической последовательности дается система показателей, связанных между собой единством процесса, явления

Правила построения рядов динамики

При составлении ряда динамики следует выполнить ряд требований.

1. Периодизация развития, т.е. расчленение ряда во времени на однородные этапы, в пределах которых показатель подчиняется одному закону развития. По существу, это типологическая группировка во времени. Периодизация может осуществляться несколькими методами.

А. Исторический метод. Периодизация осуществляется на основе “узаконенной” структуры динамики, при этом обращают внимание на значимые даты и события, а именно: время принятия управленческих решений по данному показателю, смену хозяйственного механизма, смену руководства, войны и т.п. Недостаток этого метода в том, что точные временные границы периодов путем теоретического анализа удается получить крайне редко.

Б. Метод параллельной периодизации. Идея этого метода заключается в следующем. Пусть Y –анализируемый показатель, развернутый в динамический ряд {Y_t}, где Y_t – значение уровня ряда в момент (интервал) времени t. Возможно, существует показатель X, которому соответствует динамический ряд {X_t}, определяющий поведение исследуемого показателя Y. Тогда в роли однокачественных периодов развития Y нужно взять периоды X.

В. Методы многомерного статистического анализа. Однокачественные периоды развития явлений или процессов (здоровье населения, развитие сельскохозяйственного производства и многое другое) часто трудно получить с помощью только одного показателя. Необходима система показателей, или комплексный хронологический ряд. На основе комплексных динамических рядов (системы показателей) периодизация реализуется методом многомерной средней и методами факторного анализа.

2. Статистические данные должны быть сопоставимы по территории, кругу охватываемых объектов, единицам измерения, времени регистрации, ценам, методологии расчета. Сопоставимость по территории означает, что данные по странам и регионам, границы которых изменились, должны быть пересчитаны в старых пределах. Сопоставимость по кругу охватываемых объектов означает сравнение совокупностей с равным числом элементов. Территориальная и объемная сопоставимость обеспечивается смыканием рядов динамики, при этом либо абсолютные уровни заменяются относительными, либо делается пересчет в условные абсолютные уровни. Не возникает особых сложностей при обеспечении сопоставимости данных по единицам измерения; стоимостная сравнимость достигается системой сопоставимых цен.

3. Величины временных интервалов должны соответствовать интенсивности изучаемых процессов. Чем больше вариация уровней во времени, тем чаще следует делать замеры. Соответственно для стабильных процессов интервалы можно увеличить. Так, переписи населения достаточно проводить один раз в десять лет; учет национального дохода, урожая ведется раз в год, ежедневно регистрируются курсы покупки и продажи валют, ежечасно – температура воздуха и т.п.

4. Числовые уровни рядов динамики должны быть упорядоченными во времени. Не допускается анализ рядов с пропусками отдельных уровней, если же такие пропуски неизбежны, то их восполняют условными расчетными значениями.

Показатели анализа рядов динамики

При изучении развития явления во времени встает проблема расчета средних показателей динамики и описание интенсивности изменения. Решается она построением соответствующих показателей. Для характеристики интенсивности изменения во времени такими показателями будут:

1) абсолютный прирост,

2) темпы роста,

3) темпы прироста,

4) абсолютное значение одного процента прироста.

Когда за основу сравнения берется начальный уровень ряда, получают базисные показатели. Если же сравнение производится с предыдущим уровнем, то говорят о цепных показателях. Формулы расчета показателей динамики представлены в таблице.

Показатель	Базисный	Цепной
Абсолютный прирост (i баз ; i цеп.)	Yi - Y0	Yi - Yi–1
Коэффициент роста (Кp)	Yi : Y0	Yi : Yi–1
Темп роста (Тp)	(Yi : Y0)·100	(Yi : Yi–1)∙100
Коэффициент прироста (Кпр)	Kp - 1; ;  баз : Y0	Kp - 1; ;  цеп : Yi–1
Темп прироста (Тпр)	Kпр∙100: Tp – 100	Kпp ∙ 100; Tp–100
Абсолютное значение одного процента прироста	Y0 : 100	Yi–1 : 100;  : Тпр;

17.​ Средние показатели ряда динамики.

Средний уровень ряда – это показатель, обобщающий итоги развития явления за единичный интервал или момент из имеющейся временной последовательности. Расчет среднего уровня ряда динамики определяется видом этого ряда и величиной интервала, соответствующего каждому уровню.

Для интервальных временных рядов с равными периодами времени средний уровень рассчитывается следующим образом:

или ,

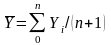где n или (n+1) – общая длина временного ряда или общее число равных временных отрезков, каждому из которых соответствует свой уровень Y_i (i = 1, 2, ..., n или i = 0, 1, 2, ..., n).

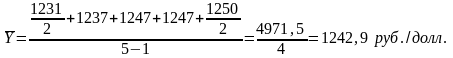
Средний абсолютный прирост рассчитывается в зависимости от способа нумерации интервалов (моментов).

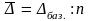или .

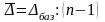Средний темп роста:

,

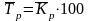Если уровни ряда нумеруются от 0 до n, то формула среднего коэффициента роста выглядит

.

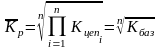Если уровни ряда нумеруются от 1 до n, то формула среднего коэффициента роста выглядит

.

Здесь К_цеп – цепные коэффициенты роста; K_баз – базисный коэффициент роста.

Средний темп прироста (%) определяется по единственной методологии:

.

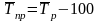Например, по данным об объемах продаж акций имеем:

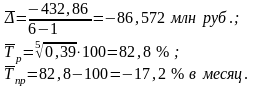
18.​ Взаимосвязанные ряды динамики, методы их статистического анализа.

Анализ взаимосвязанных рядов динамики

Под взаимосвязанными рядами динамики понимают такие, в которых уровни одного ряда в какой-то степени определяют уровни другого. Например, ряд, отражающий внесение удобрений на 1 га, связан с временным рядом урожайности; ряд уровней средней выработки связан с рядом динамики средней заработной платы; ряд среднегодового поголовья молочного стада определяет годовые надои молока и т.д. В простейших случаях анализа исчисляют коэффициенты опережения по темпам роста или прироста.

Коэффициенты опережения по темпам роста – это отношение темпов роста (цепных или базисных) одного ряда к соответствующим по времени темпам роста (также цепным или базисным) другого ряда. Аналогично находятся и коэффициенты опережения по темпам прироста

Отклонения проверяются и на наличие автокорреляции. Под автокорреляцией понимается зависимость последующих уровней ряда от предыдущих. Для проверки наличия автокорреляции используется критерий Дарбина-Уотсона:

,

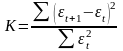где _t – отклонение фактического уровня ряда в точке t от теоретического (выровненного) значения. При К=0 имеется полная положительная автокорреляция, при К=2 автокорреляция отсутствует, при К=4 – полная отрицательная автокорреляция. Если в отклонениях от тенденции подтверждается наличие автокорреляции (положительной или отрицательной), её исключают. Это можно сделать тремя способами.

1. Для каждого из взаимосвязанных рядов динамики Х и Y получают уравнение тренда и рассчитывают отклонения:

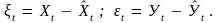
Для каждой последовательности (_t) и (_t) выполняется проверка на автокорреляцию по критерию Дарбина-Уотсона. Если значение К близко к 2, то данный ряд отклонений оставляют без изменений. Если же К заметно отличается от 2, то находят параметры уравнения авторегрессии³.

Подсчитываются новые остатки: и, в заключение, коэффициент корреляции признаков X и Y:

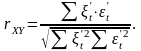
2. Корреляция первых разностей. От исходных рядов динамики Х и Y переходят к новым, построенным по первым разностям:

По Х и У определяют направление и силу связи в регрессии:

У = f(X) = С₀ + С₁·Х.

3. Включение времени в уравнение связи. У_t = f(X_t, t). В простейших случаях уравнение выглядит следующим образом:

Y_t = а₀ + а₁·X_t + a₂∙t.

19.​ Методы выявления тенденций развития в рядах динамики.

Проверка ряда на наличие тренда может выполняться несколькими методами.

1. Метод средних. Изучаемый ряд динамики разбивается на несколько интервалов (обычно на два), для каждого из которых определяется средняя величина. Выдвигается гипотеза о существенном различии средних. Если эта гипотеза принимается, то признается наличие тренда. В более мощном критерии Кокса и Стюарта весь анализируемый ряд динамики разбивают на три группы и сравнивают между собой уровни первой и последней групп.

2. Метод серий. По этому способу каждый конкретный уровень временного ряда считается принадлежащим к одному из двух типов

3. Графический метод. Для подтверждения наличия или отсутствия тренда часто достаточно представить уровни временного ряда на графике (см. тему «Статистические графики»). Графическая иллюстрация развития во времени считается достаточно убедительной.

Непосредственное выделение тренда может быть выполнено тремя методами.

1. Укрупнение интервалов. Ряд динамики разделяют на некоторое достаточно большое число равных интервалов. Если средние уровни по интервалам не позволяют увидеть тенденцию развития явления, переходят к расчету средних уровней за большие промежутки времени, увеличивая длину каждого интервала (одновременно уменьшается количество интервалов).

2. Скользящая средняя. В этом методе исходные уровни ряда заменяются средними величинами, которые получают из данного уровня и нескольких симметрично его окружающих. Количество уровней, по которым рассчитывается среднее значение, называют интервалом сглаживания. Интервал может быть нечетным (3, 5, 7 и т.д. точек) или четным (2, 4, 6 и т.д. точек). При нечетном сглаживании каждое полученное среднее арифметическое значение закрепляют за серединой интервала. При обработке ряда четными интервалами их искусственно делают нечетными, для чего образуют ближайший больший нечетный интервал, но из крайних его уровней берут только по 50 %; полученное среднее арифметическое значение также закрепляют за серединой каждого расчетного интервала. Последовательно передвигая интервал сглаживания получают последовательность средних (скользящих) значений.

3. Аналитическое выравнивание. Под этим понимается определение аналитического выражения, формулы – f(t) для основной проявляющейся во времени тенденции развития изучаемого явления. Развитие предстает как бы в зависимости только от течения времени t. Отклонения конкретных уровней ряда от уровней, соответствующих общей тенденции, объясняют действием факторов, проявляющихся случайно или циклически.

Трендовая модель имеет вид

У_t = f(t) + _t ,

где f(t) – уровень, определяемый тенденцией развития (трендовая составляющая); _t – случайное и циклическое отклонение от тенденции

В процессе аналитического выравнивания определяется конкретный вид и параметры аналитической зависимости f(t). На практике по имеющемуся временному ряду задают вид и находят параметры функции f(t), а затем анализируют поведение отклонений от тенденции. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса.

20.​ Сезонные колебания в рядах динамики: понятие, статистические методы их изучения.

Если в анализируемой временной последовательности наблюдаются устойчивые систематические отклонения от тенденции, то можно предположить наличие в этом ряду некоторых (одного или нескольких) колебательных процессов. Это особенно заметно, когда изучаемые явления имеют сезонный характер, – возрастание или убывание уровней повторяется регулярно с интервалом в один год (например, производство молока и мяса по месяцам года, потребление топлива и электроэнергии для бытовых нужд, сезонная продажа товаров и т.д.).

Уровень сезонности оценивается с помощью индексов сезонности и гармонического анализа

Индексы сезонности показывают, во сколько раз фактический уровень ряда в момент или интервал времени t больше среднего уровня либо уровня, вычисляемого по уравнению тенденции f(t). При анализе сезонности уровни временного ряда показывают развитие явления по месяцам (кварталам) одного или нескольких лет. Для каждого месяца (квартала) получают обобщенный индекс сезонности как среднюю арифметическую из одноименных индексов нескольких лет. Индексы сезонности – это, по существу, относительные величины координации, когда за базу сравнения принят либо средний уровень ряда, либо уровень тенденции. Способы определения индексов сезонности зависят от наличия или отсутствия основной тенденции.

Если тренда нет или он незначителен, то для каждого месяца (квартала)

,

где У_t – уровень показателя за месяц (квартал) t; У_ср – общий средний уровень показателя. Для обеспечения устойчивости показателей можно взять больший промежуток времени. В этом случае за Т лет рассчитывают:

,

где – средний уровень показателя по одноименным месяцам за ряд лет.

Другим методом изучения уровня сезонности является гармонический анализ. Его выполняют, представляя временной ряд как сумму гармонических колебательных процессов. Для каждой точки этого ряда справедливо выражение

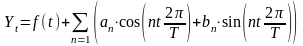, t=1, 2, .... Т.

Здесь Y_t – фактический уровень ряда в момент (интервал) времени t; f(t) – выровненный уровень ряда в тот же момент (интервал) t; a_n, b_n – параметры колебательного процесса (гармоники) с номером n. Эти параметры в совокупности оценивают размах (амплитуду) отклонений от общей тенденции и сдвиг колебаний относительно начальной точки.

Общее число колебательных процессов, которые можно выделить для ряда, состоящего из Т уровней, равно Т/2. Обычно ограничиваются меньшим числом наиболее важных гармоник. Расчеты параметров гармоники достаточно трудоемки и выполняются в настоящее время на компьютерах по известным формулам математического анализа. Аппарат гармонического анализа позволяет оценить роль каждого колебательного процесса в общей вариации уровней временного ряда. Удельный вес гармоники с номером n определяется как d_n = Д_n / Д, где Д – дисперсия ряда, рассчитанная обычным способом; Д_n–дисперсия, вносимая колебательным процессом (гармоникой) с номером n:

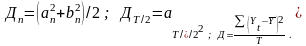
21.​ Агрегатный индекс как основная форма общих индексов.

Если известно, что изучаемое явление неоднородно и сравнение уровней можно провести только после приведения их к общей мере, анализ выполняют посредством так называемых общих индексов. Индекс выступает как общий, когда в расчетной формуле показывается неоднородность изучаемой совокупности. Примером неоднородной совокупности является общая масса проданных товаров всех или нескольких видов. Тогда сумму выручки можно записать в виде агрегата (суммы произведений взвешивающего показателя на объемный), например:

Q = р∙q.

Отношение агрегатов, построенных для разных условий, дает общий индекс показателя в агрегатной форме. Так, например, получают индекс динамики общего объема товарооборота в агрегатной форме:

Прирост товарооборота объясняется изменением уровня цен и количества проданных товаров. Влияние на прирост товарооборота общего изменения цен выражается агрегатным индексом цен I_p, который в предположении первичности изменения количественного показателя (q) и вторичности – качественного (р) имеет вид

Влияние на прирост товарооборота изменения количества проданных товаров отражается агрегатным индексом физического объема I_q, который строится также в предположении первичности изменения количественных показателей (q) и вторичности влияния качественных (р):

В форме мультипликативной индексной модели динамика товарооборота будет выражаться соотношениями

I_Q = I_q · I_p или Q₁ = Q₀ · I_q · I_p ,

где Q₀ = p₀·q₀; Q₁ = p₁·q₁.

Общий прирост товарооборота будет распределяться по факторам следующим образом: Q(q) = Q₀·(I_q-1); Q(p) = Q₀∙I_q∙(I_р - 1).

Если же принимается предположение об обратной последовательности влияния факторов – сначала р, затем q, то меняются и формулы разложения прироста и формулы расчета индексов I_q и I_р. Тогда

Q(q) = Q₀∙I_p∙(I_q – 1);

Q(p) = Q₀∙(I_р – 1).

где I_p = (p₁∙q₀)/(p₀∙q₀); I_q = (p₁∙q₀)/(p₀∙q₀).

(Отдельные слагаемые общего изменения итогового показателя можно, в принципе, получить и как разности числителя и знаменателя в формулах соответствующих агрегатных индексов).

Примером мультипликативной индексной модели с большим числом факторов является изменение общей суммы материальных затрат на производство продукции. Сумма затрат зависит от количества выпущенной продукции (индекс I_q), удельных расходов (норм) материала на единицу продукции (индекс I_n) и цены на материалы (индекс I_р). Прирост общей суммы затрат распределяется следующим образом:

M(q) = M₀·(I_q – 1);

М(n)=М₀·I_q·(I_n – 1);

М(р)=М₀·I_q·I_n ·(I_p – 1).

где М₀ = q₀·n₀·р₀, а величины индексов таковы:

индекс увеличения суммы затрат в связи с изменением объемов производства продукции (индекс физического объема)

;

индекс изменения суммы затрат за счет изменения удельных расходов материала (индекс удельных расходов)

;

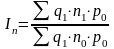индекс изменения общей суммы затрат, объясняемого изменением цен на материалы (индекс цен на материалы)

.

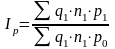Приведем формулы некоторых агрегатных индексов наиболее употребляемых в экономическом анализе.

Индекс изменения общей суммы затрат на производство продукции в зависимости от объема производства (q) и затрат на единицу (z):

.

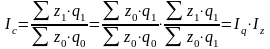Индекс изменения фонда оплаты труда в связи с изменением общей численности персонада (Т) и заработной платы (f):

.

Индекс изменения объема продукции в связи с изменением численности работающих (Т) и уровня их выработки (w):

.

Индекс изменения объема продукции в связи с изменением объема основных производственных фондов (Ф) и показателя эффективности их использования – фондоотдачи (Н).

.

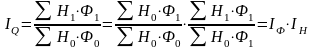Аналогичным образом находят общие агрегатные индексы и по многим другим экономическим показателям. Используемые в приведенных формулах индексы I_q, I_Т, I_Ф получаются по методу индекса физического объема, а индексы I_z, I_f, I_w, I_H, – по методу индекса цен. Таким образом, рассмотренная выше методика полностью приложима к анализу прироста продукции, изменения общих затрат на производство, изменения общего фонда оплаты труда и т.д.

22.​ Общие индексы как средние из индивидуальных индексов.
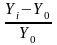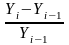