38. Ошибки репрезентативности и их применение в биометрии.

Биометрия- наука о применении математических методов в биологических исследованиях.

В практичес­кой работе основные параметры совокупности х и а вычисляют не по генеральной совокупности, а по выборке; вследствие этого возни­кают ошибки, называемые ошибками выборочности (ошибки репрезентативности). В связи с этим величины, х и а, вычисленные при изучении выборки, в некоторой степени отлича­ются от тех их значений, которые были бы получены для генераль­ной совокупности. Поэтому приходится оценивать степень точности выводов, основанных на анализе выборочных данных, вычисляя для этого ошибки статистических показателей.

39. Определение достоверности разности между средними арифметическими двух выборочных совокупностей.

При сравнении средних арифметических двух генеральных со­вокупностей любая разность между ними будет достоверна. В ве­теринарии, зоотехнии приходится сравнивать между собой средние величины не генеральных совокупностей, а выборочных (породы, линии, семейства, опытная и контрольная группы и т. д.). Поэтому необходимо установить достоверность разности между средними двух групп. Недостаточно, например, знать, что 20 дочерей какого-то производителя превосходят по удою своих матерей. Следует вычислить критерий достоверности разности, чтобы с определенной вероятностью судить о том, что следующие 100, 200 и т. д. дочерей этого производителя также будут превосходить по молочности своих матерей в аналогичных условиях. Для оценки достоверности разности между средними арифметическими двух выборочных совокупностей применяется критерий достоверности t

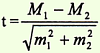где t - критерий достоверности,  m₁ и m₂ - ошибки репрезентативности,  М₁ и М₂ - средние величины

40. Коэффициенты корреляции и регрессии

Коэффициент корреляции показывает степень статистической зависимости между двумя числовыми переменными. Он вычисляется следующим образом:

,

где n – количество наблюдений, x ,y – средние значения. Значения коэффициента корреляции всегда расположены в диапазоне от -1 до 1 и интерпретируются следующим образом:

• если коэффициент корреляции близок к 1, то между переменными наблюдается положительная корреляция. Иными словами, отмечается высокая степень связи входной и выходной переменных. В данном случае, если значения входной переменной x будут возрастать, то и выходная переменная также будет увеличиваться;

• если коэффициент корреляции близок к -1, это означает, что между переменными наблюдается отрицательная корреляция. Иными словами, поведение выходной переменной будет противоположным поведению входной. Если значение x будет возрастать, то y будет уменьшаться, и наоборот;

• промежуточные значения, близкие к 0, будут указывать на слабую корреляцию между переменными и, соответственно, низкую зависимость.

Коэффициент регрессии показывает, насколько изменяется один признак при изменении другого на единицу.

 или 

41 Вопрос

Коэффициент регрессии показывает насколько в среднем изменяется один из признаков, если другой, связанный с ним изменяется на еденицу.

Rх/у=r* σх/σу. Коэффициент регрессии имеет тот же знак что и коэффициент корреляции, и измеряется в тех величинах а каких измеряется и признак.