3.6.1.1.Алгоритм spt

В системах оперативной обработки в качестве основного критерия эффективности используется средне время обслуживания заявок. Нетрудно видеть, что в случае, когда времена решения задач априори известны, минимальное среднее время ответа дает алгоритм SPT (Shortest-processing-task-first), назначающий задачи на решение в порядке убывания времени решения t_i, то есть t₁t₂...t_L . При этом время ответа u_i для задачи z_i есть u_i=  t_j, где  t_j- время ожидания , t_i - собственно время решения и среднее время ответа есть .

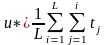Покажем, что u* действительно минимальное значение среднего времени обслуживания. Для того чтобы показать, что u* действительно минимально среди u для всех перестановок, достаточно показать, что применение к произвольной перестановке (₁,...,_L) любой парной транспозиции, меняющей местами элементы _k и _l, где t_l t_k и l>k, может лишь уменьшить исходное значение u, соответствующее перестановке (₁,...,_L), где _i - номер задачи, назначаемой на решение i-й по порядку, i=I,L. Действительно, пусть задачи с номерами _k и _l поменялись местами. Тогда для полученной перестановки среднее время обслуживания равно

Нетрудно видеть, что

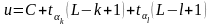, а потому

,

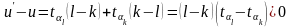так как l > k, а t_l  t_k. Следовательно, перемещение вперед задачи с меньшим временем решения приводит к уменьшению среднего времени обслуживания. В перестановке (1, ... ,L) при условии, что t₁ ... 7t_L, нельзя сделать ни одной такой улучшающей транспозиции, а потому u* есть минимальное среднее время обслуживания и алгоритм SPT дает оптимальное решение рассматриваемой задачи.

3.6.1.2.Алгоритм RR

В реальных системах оперативной обработки априорная информация о временах решения задач, как правило, отсутствует. Чтобы воспользоваться принципами планирования на основе алгоритма SPT, в систему вводятся средства, обеспечивающие выявление коротких и длинных работ непосредственно в ходе вычислительного процесса.

Простейшее правило планирования работ, обеспечивающее выполнение указанного требования, задается алгоритмом циклического обслуживания, или, иначе, алгоритмом RR (Round–Robin). Работа алгоритма иллюстрируется рисунком 3.10.

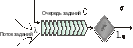
Рисунок 3.10 - Циклическое обслуживание заданий

Заявки на выполнение работ поступают с интенсивностью  в очередь , откуда они выбираются и исполняются процессором Пр. Для обслуживания отдельной заявки отводится постоянный квант времени q, достаточный для выполнения нескольких тысяч операций. Если работа была выполнена за время q, она покидает систему. В противном случае она вновь поступает в конец очереди и ожидает предоставления ей очередного кванта процессорного времени.

Оценим среднее время ожидания и пребывания работ в системе с циклическим планированием. Воспользуемся для этого аппаратом теории массового обслуживания. Для упрощения последующих выкладок предположим, что длительность кванта - не постоянная величина, а случайная, распределенная по экспоненциальному закону с тем же средним значением q. Примем также, что на вход системы поступает простейший поток с интенсивностью  работ в единицу времени, и с вероятностями  или (1-) работа не будет или соответственно будет завершена в текущем кванте. Из последнего предположения следует, что вероятность того, что работа будет выполнена точно за k квантов (не завершена за первые k-1 квантов и завершена в k-том варианте), описывается геометрическим распределением

p_k=^k-1(1-), k=1,2,...

со средним

Таким образом, если известны средняя трудоемкость работ  и длительность q кванта, то среднее количество квантов, с одной стороны, равно /q, а с другой – полученному выше выражению, то есть

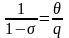, откуда .

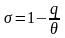Определим среднее время ответа для работы J, требующей ровно  единиц времени обработки. Пусть m – наименьшее целое, при котором m_q (то есть m – число квантов, достаточное для обслуживания заявки). Рассмотрим состояние системы на момент поступления работы J. При поступлении работы J в системе в среднем находится W₁ других работ. Значение N₁ определяется как среднее число заявок в системе с бесприоритетным обслуживанием, на вход которой заявки поступают с интенсивностью

^ⁿ

(с учетом интенсивности поступления заявок на дообслуживание в последующих тактах) и обслуживаются по экспоненциальному закону со средним q. Для определения W₁ требуется найти распределение вероятностей {pk} того, что в очереди будет ровно k заявок. Тогда

W₁=  kp_k.

Для определения p_k составим систему дифференциальных уравнений Колмогорова с помощью графа переходов (рисунок 3.11).

(q)

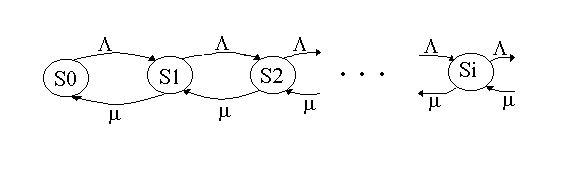
Рисунок 3.11 – Граф состояний (переходов)

Здесь S_i – состояние системы с i заявками в очереди (одна из них обслуживается). Тогда система уравнений имеет вид

p`_i =p_i-1 - p_i - p_i + p_i+1,

или



 p`_i =p_i-1 - (+)p_i + p_i+1, i=1,2,...

 p`₀ = -p₀ + p₁.

Кроме того, требуется соблюдение условия нормировки

.

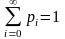Рассмотрим установившийся режим, то есть считаем, что t. Тогда вместо дифференциальных уравнений получаем алгебраические

p_i-1 - (+)p_i + p_i+1=0, i=1,2,...

p₀ + p₁=0,

p_{0 +} p_{1 +} ... + p_i + ... =1.

Из второго уравнения выразим p₁ через p₀ :

p₁ = * p₀ ;

подставим это значение в первое уравнение с i=1. Тогда

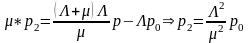
Делаем индуктивное предположение: 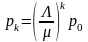. Тогда из k-го уравнения получаем

откуда 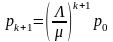, что подтверждает индуктивное предположение. Поэтому в соответствии с условием нормировки получим

где

.

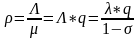На основании полученного выражения

С учетом допущения об экспоненциальности распределения кванта q время дообслуживания работы J не зависит от этого момента и в среднем равно q. Таким образом, работа будет ожидать W_1q единиц времени до получения первого кванта. За время W_1q и первый квант выполнения работы J в систему поступит  новых работ. Кроме того, W₁ работ из их общего числа W₁ вернутся обратно в очередь на довыполнение. Поэтому в следующем цикле работа J застанет в системе W₂ работ:

W₂ = W₁q + q + W₁.

Подставляя в последнее выражение ранее полученное значение W₁, получаем

В общем случае аналогично получаем

W_i =  W_i-1q + q +  W_i-1 = /(1-).

Среднее время ожидания для работы J, время выполнения которой составляет m квантов, равно

_m = q 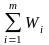= mq/(1-) .

Здесь среднее время ожидания _m определяется как время, необходимое для обслуживания всех W_i работ, стоящих впереди работы J в каждом из m циклов обслуживания. Среднее время ответа для работы J

Um = _m +mq = mq/(1-),

где  = q/(1-) = q/(q/) =  – загрузка системы. Из выражения для времени ожидания _m видно, что время ожидания обслуживания возрастает с увеличением трудоемкости mq задачи. В то же время при обслуживании задач в порядке поступления без прерываний среднее время ожидания  не зависит от трудоемкости и составляет

,

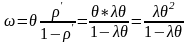где 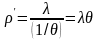, 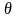– средняя трудоемкость.

Сравним  и _m:

Из последнего выражения видно, что время ожидания длинных задач (mq>) больше, чем при обслуживании в порядке поступления, а время ожидания коротких задач (mq<) – меньше времени ожидания в режиме без прерываний.