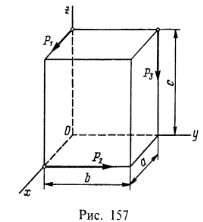
28 Приведение пространственной системы сил к простейшему виду
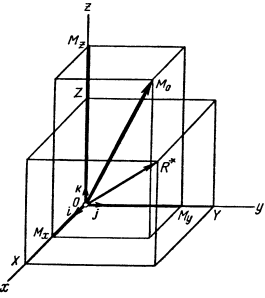
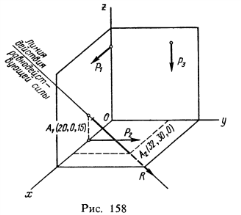
Для вычисления главного вектора и главного момента системы сил, произвольно расположенных в пр-ве, воспользуемся методом проекций.
Его проекции на оси x,y,z, проведенные через точку О, равны главным моментам системы сил относительно этих осей:
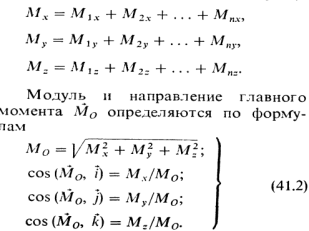
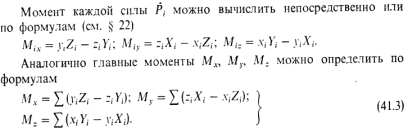
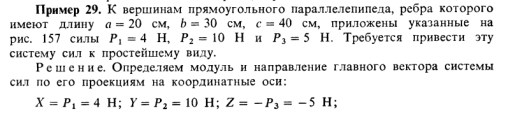
29 Центр параллельных сил и его координаты
Точка С называется центром параллельных сил. Через эту точку проходит линия действия равнодействующей заданной системы параллельных сил, если, не изменяя модулей сил, поворачивать линии действия сил вокруг точек их приложения на один и тот же угол в одну и ту же сторону.(р.1)
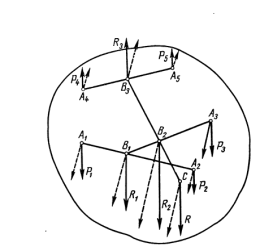р.1
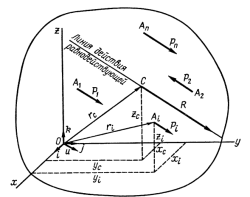р.2
Координаты центра параллельных сил(р.2)
Спроектировав
векторы левой и правой частей равенства
на
оси координат, получим формулы для
вычисления координат
центра параллельных сил:
.
Координаты точки приложения каждой силы имеют тот или другой знак, и параллельные силы, направленные в одну сторону, считаются положительными, а направленные противоположно-отрицательными. Т.о., координаты Xi,Yi,Zi и значения сил Pi в этих формулах являются алгебраическими величинами.
Выбор направления, вдоль которого параллельные силы считаются положительными, произволен и на результатах вычисления координат по формулам не отражается.
32 Центр тяжести -дуги окружности. Возьмем дугу АВ окружности радиусом R с центральным углом 2α. Так как ось х является осью симметрии этой дуги, то центр тяжести дуги лежит на этой оси и положение его определяется только координатой Xc.
Xc=(∑Xi*∆Li)/L
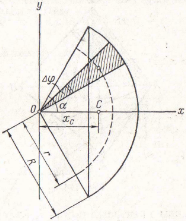
Длина дуги L = R2α, где 2α — центральный угол в радианах.
Разбиваем всю дугу на бесконечно малые элементы длиной ∆Li и вычисляем координату Xc: Xc=1/L*(∑Xi*∆Li)=1/L*(∑(Xi/cosφi)*∆Licosφi)=1/L*(∑R*∆Yi)=R/L*∑∆Yi=R/L*AB=R*(2Rsinα/2Rα).Xc=R*(sinα/α), где α — половина центрального угла в радианах.
Так как sinα < α, то центр тяжести дуги лежит внутри сектора АОВ.
34Центр тяжести площади сектора круга. Разбиваем сектор круга, соответствующий центральному углу 2α, на бесчисленное множество элементарных секторов.
Каждый элементарный сектор можно рассматривать как треугольник высотой R и основанием R∆φ, центр тяжести которого находится на расстоянии 2/3*R от центра круга.
Очевидно, что центр тяжести площади сектора AОВ совпадает с центром тяжести дуги окружности радиусом r= 2/3*R.
Xc=r*(sinα/α) или Xc=2/3*R*(sinα/α).
30 Центр тяжести твердого тела
Для тел размеры которых малы по сравнению с Земным радиусом, силы тяжести действующие на частицы тела можно считать параллельными друг к другу и сохраняющими для каждой частицы постоянную величину при любых поворотах тела.
Поле тяжести в котором выполняются эти 2 условия называются однородным полем тяжести.
Центром тяжести ТТ называется неизменно связанная с этим телом точка, через которую проходит линия действия равнодействующ. Сил при любом положении тела в пр-ве.
Обозначим силы притяжения отдельных элементарных частиц тела к Земле ∆G1,∆G2, ... , ∆Gn, вес тела G, координаты его центра тяжести
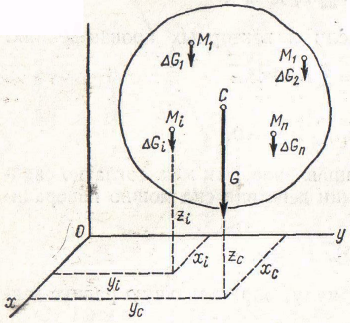
Хс, Ус, Zс, а координаты любой частицы твердого тела — Xi,Yi,Zi. Координаты центра тяжести твердого тела можно определить как координаты центра параллельных сил.
Для центра тяжести формулы:
Xc=(∑Xi*∆Gi)/G; Yc=(∑Yi*∆Gi)/G;
Zc=(∑Zi*∆Gi)/G.
В этих формулах алгебраическими величинами являются только координаты точек, а значения ∆Gi всегда положительны, так как все силы направлены в одну сторону.
По формулам этим формулам можно также вычислять координаты центра тяжести тела, разбивая его не на элементарные частицы, а на отдельные части веса Gi, координаты Xi, Yi,Zi центров тяжести которых известны.
Центр тяжести однородного тела. Вес однородного тела определяется формулой G = ᵞ * V, где V — объем тела, ᵞ — вес единицы объема.
Вес каждой частицы определяется по формуле ∆Gi = ᵞ *∆Vi , где ∆Vi-объем элементарной частицы Мi тела.
Xi,Yi,Zi -координаты центра тяжести этой частицы.
Xc=(∑Xi*∆Gi)/G=(∑Xi* ᵞ *∆Vi)/ ᵞ * V = (ᵞ *∑Xi*∆Vi)/ ᵞ * V,
Xc=(∑ Xi*∆Vi )/V,Yc= (∑Yi*∆Vi )/V ,Zc=(∑Zi*∆Vi )/V .
Центр тяжести однородного тела, заполняющего некоторый объем, называется центром тяжести этого объема.
Для однородной пластины. Xc=(∑Xi*Si)/∑Si, Yc=(∑Yi*Si)/∑Si
Для однородной пространственной линии. Xc= =(∑Xi*Li)/∑Li, Yc=(∑Yi*Li)/∑Li, Zc=(∑Zi*Li)/∑Li.