25. Выражение для моментов силы относительно координатных осей
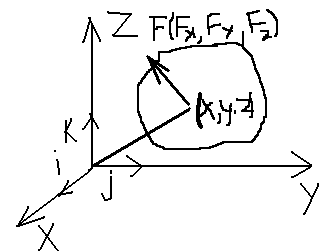
i j k
M(F)= x y z = РАСПИСАТЬ МАТРИЦУ!
F(x) F(y) F(z)
r=ix+jy+kz
M=Mxi+Myj+Mzk
Mo(F)= Mx^2+My^2+Mz^2(под корнем )
Система: Mx=(y*Fz-z*Fy)
My=(Fx*z-Fz*x)
Mz=(Fy*x-Fx*y)
cos (M,i)=Mx/MoF
cos (M,j)=My/MoF
cos (M,k)=Mz/MoF
24.момент силы относительно оси. зависимость между моментами силы относительно точки и оси, проход. через эту точку.
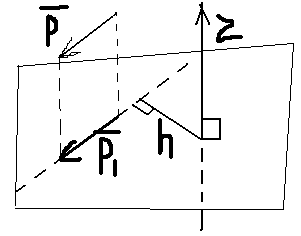
Pz(P)=+-P1*h
Тоесть, момент силы Р относительно оси OZ называется взятое с «+» или с «-» произведение модуля проекции Р1 силы Р на плоскость , перпендикулярную оси OZ на ее плечо h.(относительно точки о-пересечение оси с плоскостью)
Момент силы относительно оси равен нулю в 2-ух слу4аях:
когда Р1=0(линия действия силы Р параллельна оси)
когда сила и ось лежат в одной плоскости
зависимость между моментами силы относительно точки и оси, проход. через эту точку.
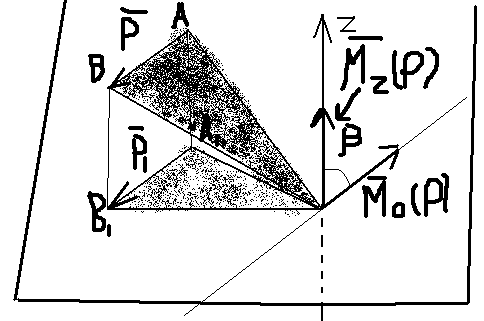
момент силы относительно оси Z:
27.
Уравнения равновесия сил, произвольно
расположенных в пространстве
1)
Σ Fx
= 0 Σ
Fy
= 0 Σ
Mi
= 0
Mx
= 0
Fx
= 0
My = 0 Fy = 0
Mz = 0 Fz = 0
26 Теорема о параллельном переносе силы
Приведение пространственной системы сил к данному центру решается с помощью теоремы о параллельном переносе силы. Любая система сил, действующих на абс.тв.тело, при приведении к произвольно взятому центру О заменяется одной силой R, равной главному вектору системы и приложенной в центре приведения О, и одной парой с моментом МО, равным главному моменту системы относительно центра О (главный вектор – векторная сумма всех сил, приложенных к телу; главный момент относительно центра –векторная сумма моментов всех сил, приложенных к телу относительно того же центра)
Приведение
произвольной пространственной системы
сил к данному центру. Главный вектор и
главный момент. Систему
сил, приложенных к телу, можно упростить,
используя теорему о параллельном
переносе силы. В результате приведения
произвольной пространственной системы
сил к данному центру в общем случае
получаем главный вектор, равный
геометрической сум-ме всех сил системы,
и главный момент, равный геометрической
сумме момен-тов всех приводимых сил
относительно центра приведения (рис.
1.33).
Сложим 
и
т.д., получим силовой многоугольник,
где
(1.15)
Затем
векторно сложим векторы моментов
(1.16)
; 
(1.17)
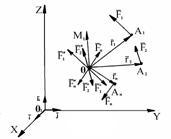
Главный вектор инвариантен по отношению к центру приведения. Главный момент зависит от вы-бора центра приведения. По модулю главный вектор вычисляется
R*=
где
проекции
главного вектора на координатные
оси 
*(Rx,
Ry, Rz), а проекции каждой из сил 
(X1,
Y1 , Z1), 
(X2,
Y2, Z2) и т.д.
Направление
находим по направляющим косинусам
Главный
момент 
Для равновесия произвольной пространственной системы сил необходимо и дос-таточно, чтобы алгебраическая сумма проекций всех этих сил на каждую из коор-динатных осей равнялась нулю, и чтобы алгебраическая сумма моментов всех сил системы относительно каждой из трех координатных осей равнялась нулю.
Система параллельных сил. Если ось OZ параллельна силам, то три уравнения (1.23) обращаются в тождества, так как проекции сил на оси OX и OY и их моменты относительно оси OZ равны нулю. Оставшиеся три уравнения явля-ются уравнениями равновесия параллельных сил в пространстве (рис. 1.34).
Для параллельных сил расположенных в плоскости XOY (рис. 1.35), имеем два уравнения равновесия:
