20 Трение скольжения и его законы. Угол и конус трения.(без рисунков.)

ПРИ СТРЕМЛЕНИИ ДВИГАТЬ ОДНО ТЕЛО ПО ПОВЕРХНОСТИ ДРУГОГО В ПЛОСКОСТИ СОПРИКОСНОВЕНИЯ ТЕЛ ВОЗНИКАЕТ СИЛА СОПРОТИВЛЕНИЯ ИХ ОТНОСИТЕЛЬНОМУ СКОЛЬЖЕНИю, называемая силой трения скольжения.

Рис.

Возникновения трения обусловлено в первую очередь шероховатостью поверхностей, создающей сопративление перемещению и наличием сцепления у прижатых друг к другу тел.

Трение покоя.

Рис

Сила трения покоя направлена в сторону, противоположную возможным движениям тела.

Сила трения покоя.

F(тр.пок)<= f* N

f-безмерная величина, наз. коэфицентом трения покоя.

После выхода тела из положения равновесия сила трения покоя уменьшается и при движении практически постоянна, и называется сила трения скольжения.

Законы трения.

Сила трения скольжения направлена в сторону, противоположную движению.

Сила трения не зависит от площадей соприкосающихся поверхностей.

Максимальная сила трения пропорциональна норм. давлению. Fmax=F*N

Коэфицент трения скольжения зависит от материала и физического состояния трущихся поверхностей.

Рис

Fтр=P

F= Fтр/N= Fтр/G=P/G

Дерево по дереву 0,4-0,7

Металл по металлу 0,15-0,25

Сталь по льду 0,027

Угол и конус трения

При наличии трения полная реакция шероховатой поверхности отклонена от нормали поверхности на некоторый угол ФИ, который в случае выхода тела из равновесия достигает максимума и наз. углом трения.

Рис

Тангенс угла трения равен коэфиценту трения

Если ФИ>АЛЬФА , то тело сдвигается с места

Если ФИ<АЛЬФА, то тело не сдвигается

Конус трения

К.Т.- конус, описанный полной реакцией R вокруг направления нормальной реакции

Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы равнодействующая активных сил находилась внутри конуса трения или проходила по образующей конуса.

22. Равновесие при наличии трения.

Величина силы статического трения всегда удовлетворяет условию:

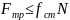, где 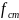- статический коэффициент трения.

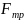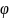Благодаря наличию силы трения между данным телом и опорной поверхностью полная реакция R шероховатой поверхности есть равнодействующая двух сил: нормальной реакции N и силы трения . Угол   между направлениями нормальной реакции  и полной реакции шероховатой поверхности R, соответствующий максимальному значению силы трения, называется углом трения.

Отсюда следует, что .

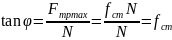Конусом трения называется поверхность, образованная линией действия R при стремлении сдвинуть тело в различных направлениях.

Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы равнодействующая активных сил находилась внутри конуса трения или проходила по его образующей.

23. Момент силы относительно центра. Момент силы относительно центра как вектор.

Под действием силы твердое тело(ТТ) может наряду с поступательным перемещение совершать вращение вокруг того или иного тела.

Вращательный эффект силы характер. ее моментом.

Перпендикуляр d опущен. из центра О на линию действия силы F относительно центра О.

Вращательный момент силы F зависит от:

- модуля силы f;

-от плеча d;

- от положения плоскости поворота ОАВ;

-направления поворота в этой плоскости

Моментом силы F относительно центра О называется величина равная взятому с соответств. Знаком произведение модуля силы на длину плеча. (М₀(F))

М₀(IF) = ±F*d? где (+)- вращение против часовой стрелки, а (-)- вращение по часовой стрелки

[М₀(F)]= Н*м

Свойства моментов

-момент силы не изменяется при переносе точки приложения

-момент силы относительно центра О равен о, тогда и только тогда , когда линия действия силы пересекает ось или когда линия действия силы и ось находятся в одной плоскости.

- момент силы численно выражается площадью тр-ка ОАВ

М₀(F)=±2*S(тр-ка ОАВ)

S(тр-ка ОАВ)= 0,5*АВ*d=0,5*I F*d I = 0.5* М₀(F)

Момент силы относительно центра как вектор

Момент силы F относит. т. О изображается вектором М₀(F), прилож. в той же точке и направлены перпендик. плоскости содержащ силу F и точку О в такую сторону, чтобы смотря на встречу этому вектору видеть силу F стремящую вращать эту пл-ть в сторону обратную вращению часовой стрелки(правило буравчика)

S(тр-ка ОАВ)=0,5* F*r*sinα

 М_о(F)=r x F =r*F*sin(r;F)

Вектор момента М₀ силы F можно рассматривать как векторное произведение радиус-вектора r, проведен. из этой точки в точку приложения силы F на вектор силы.