14 Понятие о ферме

Ф.-мометрически неизменяемая шарнирно-стержневая конструкция.

Если все стержни фермы лежат в одной плоскости, то такую ферму называют плоской.

Точки, в кот. сходятся точки оси стержней наз. узлами фермы., а те узлы, которыми ферма опирается на основание называются опорными узлами.

Рис

Формула для простой плоской фермы: n=2*m-3

n- кол-во стержней

m- кол-во узлов

Допущения , применяемые при расчете ферм:

внешние силы приложены только к узлам фермы

веса стержней принебрежительно малы

трения в шарнирах отсутствуют

Вывод: при таких допущениях, силы, действующие на узлы фермы со стороны стержней всегда направлены вдоль линий проходящих через концы стержней. Если стержни фермы прямые (прямолинейные), то они при этом либо растягиваются либо сжамаются.

15 Определение усилий в стержнях фермы методом сечений (способ Риттера)

Расчет выполняется в последовательности:

– определяются опорные реакции, если они ранее не были определены;

– ферма разрезается на две части сечением, которое проходит через стержни, усилия в которых необходимо определить; при этом должно разрезаться не более трех стержней, усилие в которых неизвестны;

– рассматривается равновесие одной из двух частей фермы; действие отброшенной части заменяется реакциями перерезанных стержней, которые направляются вдоль стержней от узлов; изображаются активные силы, действующие на рассматриваемую часть фермы;

– составляются уравнения равновесия так, чтобы в каждое уравнение входило одно неизвестное усилие.  Обычно составляются уравнения моментов сил относительно точек, где пересекаются линии действия двух неизвестных усилий. Если же на расчетной схеме два стержня параллельны, то составляется уравнение проекций сил на ось, перпендикулярную к этим стержням;

– решая каждое из составленных уравнений равновесия, находят искомые усилия в стержнях.

16 Графоста́тика — в теоретической механике учение о графическом способе решения задач статики.

Графостатика позволяет решать задачи с системами сходящихся сил. На плоскости такая система сил является статически определимой, если число неизвестных сил в ней не превышает двух.

Для плоской системы сил последовательность нахождения неизвестных сил в этом методе такова:

-выбирается масштаб сил;

-в выбранном масштабе строятся векторы известных сил, причём каждый последующий вектор откладывается из конца предыдущего;

-из конца последнего из векторов известных сил проводится прямая, параллельная одной -из двух неизвестных сил;

-из начала первого построенного вектора проводится прямая, параллельная второй неизвестной силе;

-точка пересечения двух прямых даст отрезки, эквивалентные двум неизвестным силам;

-длины полученных отрезков умножаются на масштаб — получаются значения двух искомых сил.

Чем крупнее выбранный масштаб, тем выше точность решения задачи.

18. Методика построения диаграммы Максвелла-Кремона

Диагамма предназначена для определения усилий в стержнях ферм.

Построение диаграммы заключается в соединении силовых многоугольников построенных для всех узлов фермы в один чертеж таким способом, чтобы ни одно из усилий не повторялось дважды.

Алгоритм построения диаграммы:

-Определяются опорные реакции из условия равновесия всей фермы как ТТ. Осуществляется это аналитическим методом при помощи уравнений равновесия.

-Отбрасываются опоры и изображают все приложенные к ферме силы(активные и найденные реакции связи)

-Часть плоскости, ограниченная контуром фермы и линиями действия внешних сил обозначаются буквами. Обозначаются буквами также части плоскости, ограниченные стержнями фермы, узлы фермы обозначаются римскими цифрами, стержни- арабскими цифрами.

-Строится замкнутый многоугольник внешних сил, откладывая силы втом порядке, в котором они встречаются при обходе фермы.

-Последовательно строят на этом же рисунке замкнутые силовые многоугольники для каждого узла, при этом узлы выбирают в таком порядке, чтобы каждый раз число неизвестных усилий в стержнях равнялось 2. -----Обход каждого узла производится в том направлении как для внешних сил.

-Для определения сжаты или растянуты стержни в каждом замкнутом многоугольнике мысленно представляют стрелки в одном направлении и переносят на стержни.

стрежень сжат – усилие к узлу

стержень разжат – усилие от узла.

Измеряется на диаграмме отрезки изображающие усилия в стержнях фермы и находятся усилия.

17. Определение равнодействующей системы сил с помощью веревочного многоугольника Веревочный многоугольник, построение графической статики, к-рым можно пользоваться для определения линии действия равнодействующей плоской системы сил, для нахождения реакций опор, изгибающих моментов в сечениях балки, положений центров тяжести и моментов инерции плоских фигур и т. п.

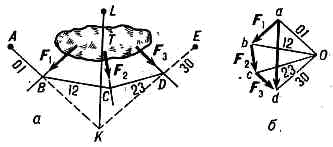
Чтобы построить В. м. для плоской системы сил F1 F2, F3, действующих на тело Т (рис., а), сначала строят из этих сил в выбранном масштабе многоугольник сил abcd (рис., б). Затем из произвольной точки (полюса) О, не лежащей на сторонах аb, bc, cd, da или на их продолжениях, проводят лучи Оа, Оb, Ос, Od, к-рые обычно обозначают цифрами 01, 12, 23, 30. После этого на рис. а из произвольной точки А проводят прямую, параллельную лучу 01, до пересечения её с линией действия силы F1 в точке В. Из точки В проводят прямую, параллельную лучу 12 до пересечения её с линией действия силы F2 в точке С и т. д. Последней проводится прямая DE параллельная лучу 30, до произвольной точки Е. Полученная таким образом фигура ABCDE и наз. М. в., построенным для системы сил F1, F2, F3 при полюсе О. Если для данных сил силовой многоугольник не замкнут (как на рис., б), то система сил приводится к равнодействующей R=ad, линия действия KL к-рой проходит через точку К, где пересекаются лучи АВ и DE. Если многоугольник сил замкнут, то крайние лучи 01 и 30 на рис., б сливаются, а крайние стороны АВ и DE M. в. параллельны и проходят в общем случае друг от друга на каком-то расстоянии h. Тогда система сил приводится к паре сия о моментом, равным произведению Oa•h, где Оа измеряется в масштабе сил, a h — в масштабе длин. Если же крайние стороны АВ и DE М. в. тоже сливаются (h=0), то и М. в. наз. замкнутым, а система сил находится в равновесии.Построение М. в. используется при нек-рых инженерных расчётах, в частности в сопротивлении материалов, статике сооружений.

21 Трение качения — сопротивление движению, возникающее при качении одного тела по поверхности другого. Проявляется, например, между элементами подшипников качения, между шиной колеса автомобиля и дорожным полотном.

Механизм трения качения объясняют деформацией соприкасающихся тел. Колесо как бы вдавливается в опору, образуя ямку, через край которой колесу все время приходится перекатываться .

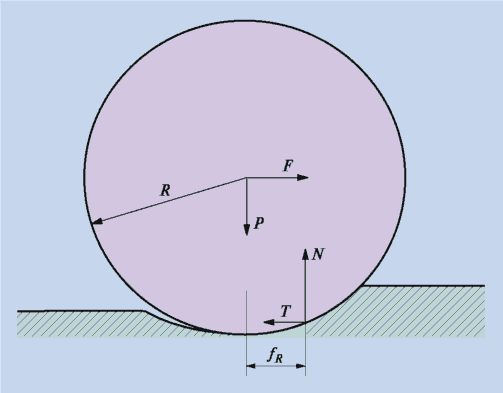
Плечо силы N, затрудняющей «выкатывание» из ямки, и есть коэффициент трения качения (измеряется в метрах ).

Коэффициент трения качения вычисляют как отношение момента трения к силе нормального давления N.

Трение верчения. Существование трение верчения можно установить экспериментально, рассматривая сферу на горизонтальной поверхности. Когда оба тела абсолютно твердые, то любая горизонтальная пара сил будет поворачивать сферу вокруг вертикальной оси. Однако из эксперимента известно, что сфера начнет поворачиваться, когда момент пары сил превысит некоторое значение 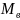 , которое определяется по выражению

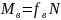
где N является силой нормального давления. Это объясняется наличием пары сил трения верчения, когда оба тела деформируются и имеют шероховатые поверхности, а их контакт происходит по малой площадке.

Коэффициент 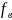  является линейной величиной, называемой коэффициентом трения верчения.