8 Теорема о параллельном переносе силы.

Ее  формулировка:

 НЕ  ИЗМЕНЯЯ  ДЕЙСТВИЯ  СИЛЫ  НА  ТВЕРДОЕ  ТЕЛО,  СИЛУ  МОЖНО  ПЕРЕНЕСТИ 

ПАРАЛЛЕЛЬНО  САМОЙ  СЕБЕ  В  ЛЮБУЮ  ТОЧКУ  ТЕЛА - ЦЕНТР  ПРИВЕДЕНИЯ,  ПРИЛОЖИВ  ПРИ  ЭТОМ  К  ТЕЛУ  ПАРУ  СИЛ  С  МОМЕНТОМ,  РАВНЫМ  

 МОМЕНТУ  ПЕРЕНОСИМОЙ   СИЛЫ  ОТНОСИТЕЛЬНО  ЦЕНТРА ПРИВЕДЕНИЯ. 

    Доказывается эта вспомогательная теорема  элегантно и просто с помощью одной из аксиом статики, позволяющей преобразовывать системы сил в эквивалентные  системы - аксиомы о том,  что к СС можно добавить любую уравновешенную СС.

ЛЮБУЮ  ПРОИЗВОЛЬНУЮ  СИСТЕМУ  СИЛ  ПРИ  ПРИВЕДЕНИИ  К НЕКОТОРОМУ  ЦЕНТРУ  ПРИВЕДЕНИЯ  МОЖНО  ЗАМЕНИТЬ  ОДНОЙ СИЛОЙ,  ПРИЛОЖЕННОЙ  В  ЦЕНТРЕ  ПРИВЕДЕНИЯ, И  ОДНОЙ  ПАРОЙ  СИЛ  С  МОМЕНТОМ,  РАВНЫМ  ГЕОМЕТРИЧЕСКОЙ  СУММЕ  МОМЕНТОВ СИЛ СИСТЕМЫ  ОТНОСИТЕЛЬНО  ЦЕНТРА  ПРИВЕДЕНИЯ.

9 Вопрос

Главный момент сил, составляющих пару, относительно любой точки в пространстве не зависит от положения этой точки и геометрически равен моменту пары сил

Главным вектором системы сил называется вектор R, равный векторной сумме этих сил:

R = F1 + F2 + ... + Fn = Fi.

Главным моментом системы сил относительно центра O называется вектор LO, равный сумме векторных моментов этих сил относительно точки О:

LO = MO(F1) + MO(F2) + ... + MO(Fn) = MO(Fi).

Вектор R не зависит от выбора центра О, а вектор LO при изменении положения центра О может в общем случае изменяться.

10. Уравнение равновесия сил, произвольно расположенных на плоскости, параллельных сил.

М = 0 R = 0 R =КОРЕНЬ КВАДР ИЗ(Px^2+Py^2) = 0

1) Σ Mi = 0 Σ Px = 0 - основное усорвие равновесия плоской

Σ Py = 0 системы сил

2) Σ Mia = 0

Σ Mib = 0 - 2-ое условие равновесия

Σ Ui = 0

U - ось

Органичение: Ось U не должна быть перпендикулярна прямой АВ

3) Σ Mia = 0

Σ Mib = 0 - 3-е условие равновесия

Σ Mic =0

Ограничение: Точки А, В и С не должны лежать на одной прямой

Уравнение равновесных параллельных сил

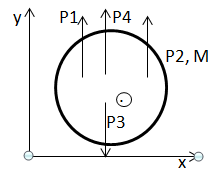
Σ Mia = 0 Σ Mib = 0 Oсобенности: АВ не должны быть параллельны силам.

11. Теорема Вариньона о моменте равнодействующей

Момент равноДействующей относительно любой точки равен геометрической сумме моментов составляющих сил относительно этой точки, а момент равнодействующей силы относительно любой оси равен алгебраической сумме моментов составляющих сил относительно этой оси.

12. Статически определимые задачи

Статически определимые задачи-это такие задачи, которые можно решать методом статики ТТ( число неизвестных не превышает число неизвестных в уравнении равновесия сил).

Статически неопределимые задачи- это задачи с числом неизвестных превышающих число уравнений равновесия сил.

Для плоской системы сил-не более 3

Для пространственной системы сил-не более 6.

13 РАВНОВЕСИЕ СИСТЕМЫ, СОСТОЯЩЕЙ ИЗ НЕСКОЛЬКИХ ТВЕРДЫХ ТЕЛ

В случае системы твердых тел, соединенных между собой, силы, действующие на эту систему, можно подразделить на две группы:

1) внешние силы;

2) внутренние силы.

Внутренними силами называются силы взаимодействия между телами, входящими в данную систему. По закону равенства действия и противодействия внутренние силы всегда попарно равны по модулю и прямо противоположны по направлению, но приложены к двум разным взаимодействующим между собой телам системы.

Внешними силами называются те силы, с которыми тела, не входящие в данную систему, действуют на тела этой системы.

Рассмотрим, например, систему, изображенную на рис. 39. Балка АВ весом  , может вращаться вокруг оси А неподвижного цилиндрического шарнира и концом В опирается свободно на другую балку CD весом  , которая подперта в точке Е и соединена со стеной шарниром  .

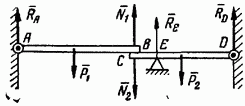
Рис. 39.

В данном случае система состоит из двух тел: балки АВ и балки  .

Внутренними силами для дгнюй системы являются силы взаимодействия между балками, т. е. сила   давления балки АВ на балку CD и сила   с которой балка CD действует на балку АВ. По закону равенства действия и противодействия силы N, и  равны по модулю и противоположны по направлению, т. е.  .

Веса   и   балок представляют собой силы, с которыми эти балки притягиваются к Земле, и, следовательно, для данной системы являются силами внешними, так как Земля по отношению к этой системе есть внешнее тело. Реакции   и  шарнирных опор А и D, а также реакция   опоры Е являются для данной системы тоже внешними силами, так как шарнирные опоры А и D и опора Е не принадлежат к рассматриваемой системе, состоящей только из двух балок.

При решении задач на равновесие системы тел необходимо учесть, что все внешние и внутренние силы, приложенные к каждому телу в отдельности, уравновешиваются. Следовательно, в случае плоской системы сил можно составить по три уравнения равновесия для каждого из этих тел в отдельности.

Таким образом, для системы, состоящей из   тел, можно составить всего   уравнений равновесия. Поэтому, если число неизвестных сил в данной задаче не более  , то такая задача является статически определенной. Если же число неизвестных в задаче окажется больше  , то такая задача не может быть разрешена только на основании уравнений статики абсолютно твердого тела и потому является статически неопределенной.

Так как внутренние силы попарно равны по величине и направлены по одной прямой в противоположные стороны, то алгебраическая сумма их моментов относительно любой точки равна нулю и сумма их проекций на любую ось также равна нулю. Поэтому, если составим уравнение равновесия (уравнение моментов относительно какой-либо точки, или уравнение проекций на какую-либо ось) для каждого тела в отдельности и затем все   уравнения сложим, то в полученном уравнении члены, содержащие внутренние силы, попарно уничтожаются и, следовательно, в это уравнение будут входить только внешние силы.

Таким образом, если система тел находится в равновесии, то внешние силы, приложенные к этой системе, удовлетворяют тем же трем уравнениям равновесия, что и в случае равновесия одного абсолютно твердого тела. Эти уравнения представляют собой условия равновесия внешних сил, действующих на систему.

Из этих уравнении можно найти все внешние реакции, если число этих внешних реакций не больше трех.

Если же число внешних реакций окажется больше трех или если в задаче, кроме внешних реакций, требуется найти неизвестные внутренние силы, то необходимо применять метод расчленения системы, т. е. нужно рассматривать равновесие каждого тела системы в отдельности и для каждого из этих тел составлять уравнения равновесия, учитывая при этом все силы, приложенные к рассматриваемому телу. Если система состоит, например, из двух твердых тел, то, применяя метод расчленения, получим в общем случае всего шесть уравнений равновесия (по три уравнения для каждого тела). Для составления шести уравнений равновесия можно применять еще и другой прием, а именно: составить сначала три уравнения для всей системы в целом (как для одного абсолютно твердого тела) и затем к этим трем уравнениям присоединить три уравнения равновесия, составленные только для одного из двух тел данной системы. Этот второй прием нередко предпочтительнее, так как в уравнения равновесия, составленные для всей системы в целом, входят только внешние силы и потому эти уравнения обычно оказываются проще.