6Теорема об условии эквивалентности пар сил в пространстве:

Пары, сил в пространстве эквивалентны, если их моменты геометрически равны.

Дано: две пары сил Р, Р' с плечом АВ=d1 и Q, Q’ лежащие в различных плоскостях и имеющие геометрически равные моменты.

Докажем, что эти пары сил эквивалентны.

Док-во: М1=Рd1_ъ М₂=Qd2 и M1=M2,(т.е. моменты пар имеют и одинаковые направления).Поэтому пары Р,Р' и Q,Q' лежат в параллельных плоскостях / и //

и стремятся вращать эти плоскости в одном и том же направлении.

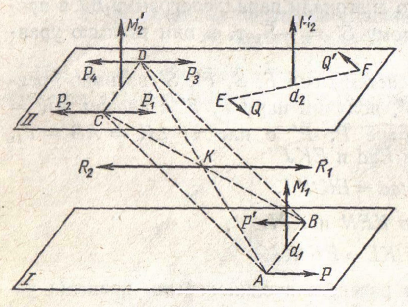
Возьмем в плоскости // отрезок СD=AB,CD//AB.К концам этого отрезка приложим по две взаимно уравновешивающиеся си­лы, равные по модулю и параллельные силам па­ры Р, Р': P1=P2=P3=P4=P.

Сложим силу Р, прило­ женную в точке А, с силой

рз, приложенной в точке D. Их равнодействующая с модулем

R1 = Р + рз приложена в точке K, делящей отрезок АD пополам, т. е. в точке пересечения диагоналей параллелограмма АВDС.

Сложив силу Р', приложенную в точке В, с силой Р₂, приложен­ной в точке С, получим их равнодействующую с модулем R₂ =Р' + Р₂, которая также приложена в точке К.. Силы R₁ и R₂, приложенные в точке K, как равные по модулю и направленные по одной прямой в противоположные стороны, взаимно уравновешива­ются. Остаются силы P1 и Р₄, составляющие пару сил с плечом CD, расположенную в плоскости //.

Эта пара сил, эквивалентная паре сил Р, Р', стремится вращать плоскость // в том же направлении, в котором пара сил Р, Р' стре-мится вращать плоскость / и имеет силы и плечо, соответственно рав­ные силам и плечу пары Р, Р'.

Так как пара P1, Р₄ имеет модуль момента

М2=P1 • СD= Рd1= Qd2 = М₂

и стремится вращать плоскость // в том же направлении, как и пара Q, Q', то согласно теореме (об усл. Эквив. Пар сил, леж. В одн. Пл-ти), пара Q, Q' эквивалентна паре P1,P4 , а следовательно, и паре Р, Р', что и требовалось доказать.

Из теоремы следует, что не изменяя действия пары сил на твердое тело, пару сил можно переносить в любую плоскость, параллельную плоскости ее действия, а также изменять ее силы и плечо, сохраняя неизменным модуль и направление ее момента.

Таким образом, вектор момента пары сил можно переносить в любую точку, т. е. момент пары сил является свободным вектором.

7 Сложение пар сил. Условие равновесия пар сил

• Вектор момента пары сил можно перенести в любую точку. Момент пар сил является свободным вектором.

• Вектор момента определяет: положение пл-ти действия пары сил, направление вращения, числовое значение момента.

Теорема: Геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары.

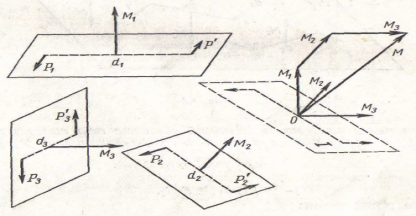
Пусть требуется сложить две пары сил, расположенные в пере­секающихся плоскостях / и //, имеющие моменты M1 и М2. Выбрав силы этих пар равными по модулю: P1=P2=P3=P4=P.Определим плечи этих пар: d1=M1/P и d2=M2/P.

Докажем, что диагональ ВF = М₁ + М₂ представляет собой мо­мент зкизалентной пары P2, Р_4. Для этого докажем, что:

1 ) ВF = Рd;

2) отрезок ВF перпендикулярен к плоскости действия эквива­лентной пары сил;

3) смотря навстречу вектору ВF, можно видеть пару Р₂, Р₄ стре­мящейся вращать плоскость в сторону, обратную вращению часовой стрелки.

Доказательство:

1. Треугольники ВАС и ВDF подобны, так как M1=Pd1; M2=Pd2;

M1/M2=d1/d2, BD/DF=BA/AC. И уголВDF=углуВАС как углы со взаимно перпендикулярными сторонами.

Из подобия этих треугольников следует, что ВF/ВD = ВС/ВА, т. е.

BF/M1=d/d1,откуда BF=M1*(d/d1)= Pd1*(d/d1)=Pd.

2. Так как вектор момента каждой пары сил перпендикулярен к плоскости действия этой пары сил, то M1┴P2, M2┴P2,а поэтому плоскость параллелограмма ВDFЕ перпендикулярна к силе |пары Р2 и ВF┴ Р₂. уголDBA = 90° и уголСBA = углуFВD, угол СВF = 90°, ВF ┴BС.

Так как диагональ параллелограмма ВF перпендикулярна к силе

пары Р₂ и к плечу пары сил ВС, то она перпендикулярна к плоскости действия эквивалентной пары сил.

3. Смотря навстречу вектору ВF, можно видеть пару Р₂,P4,стремящейся вра­щать плоскость ее действия в сторону, обратную вращению часо­вой стрелки.

Из всего следует, что вектор ВF = М, т. е. геоме­трическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары сил M1+M2=M.

Момент пары сил, эквивалентной данной системе пар сил в про­странстве, равен геометрической сумме моментов составляющих пар сил

M=M1+M2+…Mn=∑Mi(i=1,n).

Условие равновесия пар сил, произвольно расп. В пр-ве:

Пары сил, произвольно расположенные в пр-ве, взаимно уравновешиваются в том случае, если геометрическая сумма их моментов равна нулю. M=∑Mi=0