10. Плоскопараллельное движение твердого тела
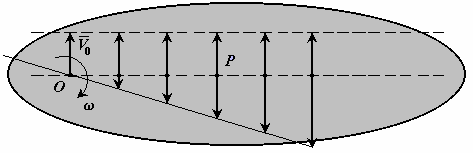
Плоскопараллельным (плоским) движением (ППД) твердого тела называется такое движение, при котором все точки тела перемещаются в плоскостях параллельных некоторой неподвижной плоскости (рисунок 2.11).
При таком движении точки, лежащие в разных плоскостях на одном отрезке, перпендикулярном неподвижной плоскости (например M1M2 ) совершают одинаковые движения.
Отрезок M1M2 движется поступательно. Поэтому изучение плоскопараллельного движения сводится к изучению движения плоской фигуры в какой-то плоскости.
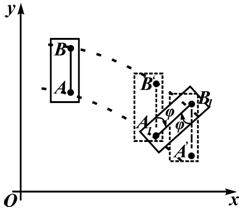
На рисунке 2.12 показано перемещение пластинки в плоской системе отсчета xOy из одного положения в другое. Такое перемещение можно осуществить двигая пластину поступательно с траекторией точки A с последующим поворотом на угол φ вокруг точки A1. Это же перемещение можно выполнить иначе.
Например, перемещая пластинку поступательно с траекторией точки B , с последующим поворотом вокруг B1 на угол φ. Траектории точек A и B различны, а угол поворота в обоих случаях одинаков.
Положение пластинки вполне определяется положением скрепленного с ней отрезка (например AB), закон движения которого можно задать в виде:
xA=xA(t), yA=yA(t), φ=φ(t).
Точка A в этом случае называется полюсом. Если принять за полюс точку B , то получим уравнения:
xB=xB(t), yB=yB(t), φ=φ(t)
За полюс выбирается точка, закон движения которой известен.
11: Теорема о скоростях точек плоской фигуры. Мгновенный центр скоростей и его определение. Частные случаи определения положения мгновенного центра скоростей
1)Скорость любой точки плоской фигуры равна геометрической сумме скорости выбранного полюса и скорости точки во вращательном движении фигуры вокруг полюса. Производная от вектора AM, постоянного по величине и переменного по направлению, численно равна скорости точки М при вращении ее вокруг точки А. Вектор V(MA)= ω⋅AM перпендикулярен отрезку АМ. Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов
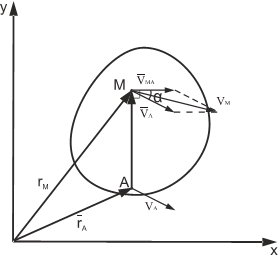
Численную величину скорости точки М можно получить, если воспользоваться теоремой косинусов
или спроецировать
векторное равенство (1) на выбранные
оси координат:
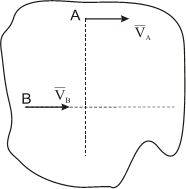
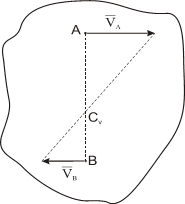
2) Мгновенным центром скоростей называется точка плоской фигуры, скорость которой в данный момент времени равна нулю. Теорема. В каждый момент времени при плоском движении фигуры в ее плоскости при ω=0 (непоступательное движение), имеется один единственный центр скоростей.
, 
, 
,
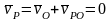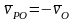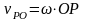следовательно
.
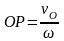Мгновенный
центр скоростей находится на перпендикуляре
к скорости
,
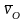проведенном из точки О, на расстоянии
.
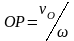Мгновенный центр скоростей это единственная точка плоской фигуры для данного момента времени. В другой момент времени мгновенным центром скоростей будет уже другая точка.
Возьмем
точку Р за полюс
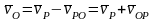
Так
как
,
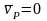то
.
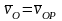Аналогичный результат получается для
любой другой точки плоской фигуры.
.
.
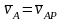
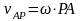
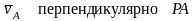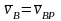
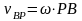
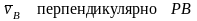Скорости точек плоской фигуры определяются в данный момент так, как если бы движение фигуры было вращением вокруг мгновенного центра скоростей.
Скорости точек плоской фигуры пропорциональны их расстояниям до мгновенного центра скоростей.
1. СV совпадает с точкой В VB=0. Шатун АВ вращается вокруг точки В
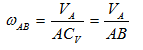
2.
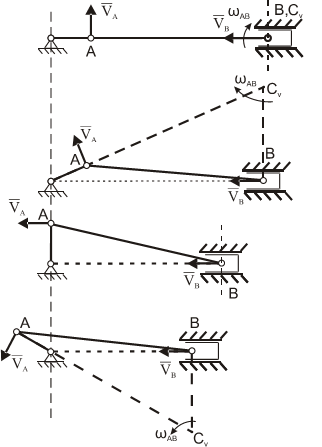
3. МЦС лежит в «бесконечности»
4.
здесь VB II VA
В этом случае МЦС находится в “бесконечности” , т.е
