3 Кинематика. Определение скорости точки при различных способах задания движения. Годограф

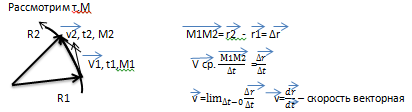
Вектор скорости точки в данный момент времени равен 1-ой производной радиус-вектора точки по времени

Определение скорости при естественном задании

V ср= =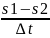

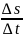
v = v=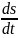 – численная величина скорости в данный момент времени равна 1-ой производной от расстояния (кривол. коорд S) по времени

2 Вопрос основные способы задания движения

Определить движение точки — это значит уметь определить положение этой точки по отношению к выбранной системе отсчета в любой момент времени .

Траектория – непрерывная линия, которую описывает движущаяся точка относительно данной системы отсчета

В кинематике применяются три способа, описывающих движение точки: векторный, координатный и естественный.

При естественном, или натуральном, способе движение точки определяется ее траекторией и уравнением движения по этой траектории:

где О — начало отсчета  на траектории, a s — дуговая координата точки М или взятая с соответствующим знаком длина дуги, отсчитываемая вдоль траектории от начала отсчета до точки М.

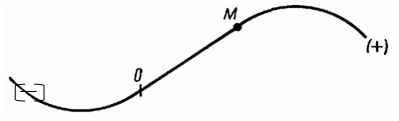
Для задания естественного способа движения необходимо знать:

1. Траекторию точки

2. Начало отсчета на тр-рии с указанием положительного и отрицательного направления

3. Закон движения точки вдоль траектории (S=f(t)), где s- путь

Полярные координаты

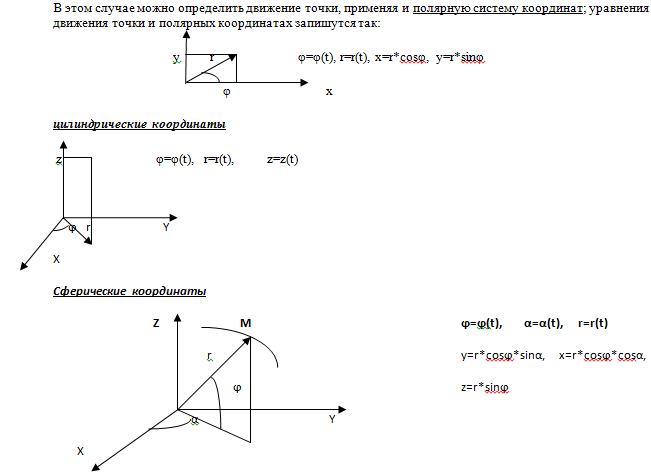
Кинематика 4 вопрос . Ускорение точки при различных способах задания движения

Ускорение- векторная величина , характеризующая с течением времени изменение модуля и направление скорости

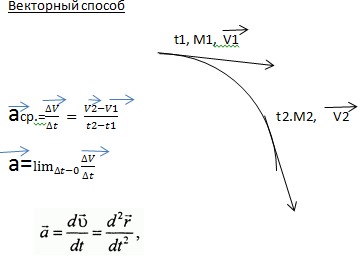
Кинематика 5 вопрос. Поступательное

движение. Уравнения скорости, ускорения и тд.

Поступательное движение твердого тела – это движение, при котором любая прямая, связанная с телом, при его движении остается параллельной своему начальному положению.

Примеры поступательного движения: движение педалей велосипеда относительно его рамы, движение поршней в цилиндрах двигателя внутреннего сгорания относительно цилиндров, движение кабин колеса обозрения относительно Земли.

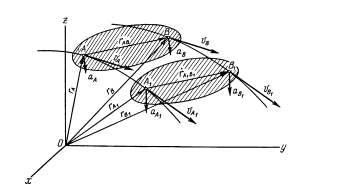
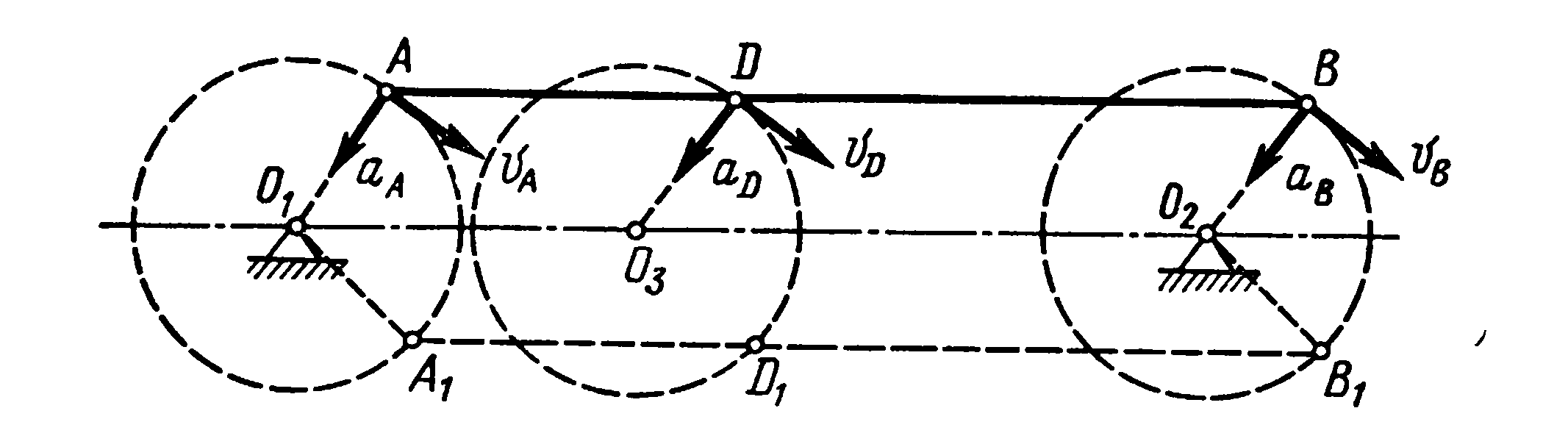
Теорема. При поступательном движении твердого тела, все точки описывают одинаковые траектории и в каждый момент времени имеют геометрически равные скорости и ускорения.

Для док-ва теоремы выберем 2 произвольные точки тела А и В и проведем из А в В радиус-вектор r_АВ

9. Передаточный механизм

Передаточные механизмы передают движение от одного тела к другому. Параметры движения тел определяются с учетом параметров точек соприкосновения (зацепления) этих тел. На рисунке 2.6 (а, б, в, г) приведены различные схемы передачи движения от одного тела к другому.

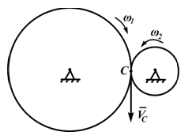
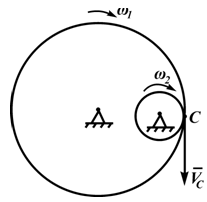
    На рисунках 2.6,а и 2.6,б зависимости угловых скоростей колес определяются из соотношения  Vc=ω₁⋅ r₁=ω₂⋅ r₂, т.е.

 

 ω₁/ω₂=r₂/r₁  (2.12)

    На рисунке 2.6,а (внешнее зацепление) колёса вращаются в противоположные стороны, на рисунке 2.6,б (внутреннее зацепление) колеса вращаются в одну сторону. 

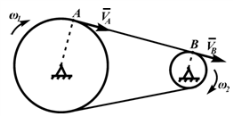
    На рисунке 2.6,в показана цепная (ременная) передача. Скорости точек  A  и B   цепи должны быть равны соответственно скоростям точек A  и B , принадлежащих шкивам:

V_A=ω₁⋅ r₁=V_B=ω₂⋅r_2,         ω₁/ω₂=r₂/r₁ . 

(2,6)

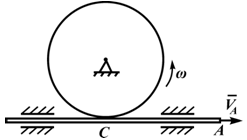
На рисунке 2.6,г поступательное движение стержня обеспечивает вращение колеса:

                                           V_A=V_C=ω⋅r,     ω=V_A/r

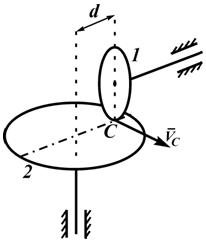
Рис. 2.7

На рисунке 2.7 изображена фрикционная передача: колесо 1, прижимаясь к торцу колеса 2 в точке C, обеспечивает его вращение вокруг вертикальной оси.

                                      V_C=ω₁⋅r₁=ω₂⋅d,  ω₁/ω₂=d/r₁