При использовании приема цепных подстановок важно обеспечить строгую последовательность подстановки. В первую очередь выявляется влияние количественных показателей, а затем – качественных.

Приём абсолютных разниц. В отличие от приёма цепных подстановок, приём абсолютных разниц применим только к мультипликативным моделям. Суть этого приёма заключается в определении абсолютных приростов факторных показателей, называемых абсолютными разницами. Измерение влияния каждого фактора осуществляется путём умножения абсолютной разницы этого фактора на базисные и/или текущие значения других факторных показателей. Достоинство данного приёма заключается в оперативности расчётов.

Пример. У = А·В·С·D.

Приём относительных разниц. Суть его состоит в расчёте относительных разниц, которые определяются как темпы прироста факторных показателей. Для измерения влияния факторов рассчитанные относительные разницы умножаются на базисное или условное значение результативного показателя. Приём относительных разниц, как и приём абсолютных разниц, применяется только к мультипликативным моделям. Его использование удобно, если в исходных данных присутствуют темпы прироста факторных показателей.

Пример. У = А·В·С·D

; ; ;

.

6. Применение приемов пропорционального деления

и долевого участия

Прием пропорционального деления. Применяется к кратным и смешанным моделям. Заключается в распределении отклонений по результативному показателю согласно удельному весу фактора, его обусловливающего, в общей сумме отклонений по факторам.

Применяется, когда имеется большое число частных показателей и зависимость их друг от друга нельзя установить.

Согласно приему пропорционального деления рассчитывается коэффициент пропорционального деления.

, ,

где F - общее изменение результативного показателя.

Оценка влияния каждого фактора путём умножения коэффициента пропорционального деления на изменение этого показателя.

Пример. У = А·В·С.

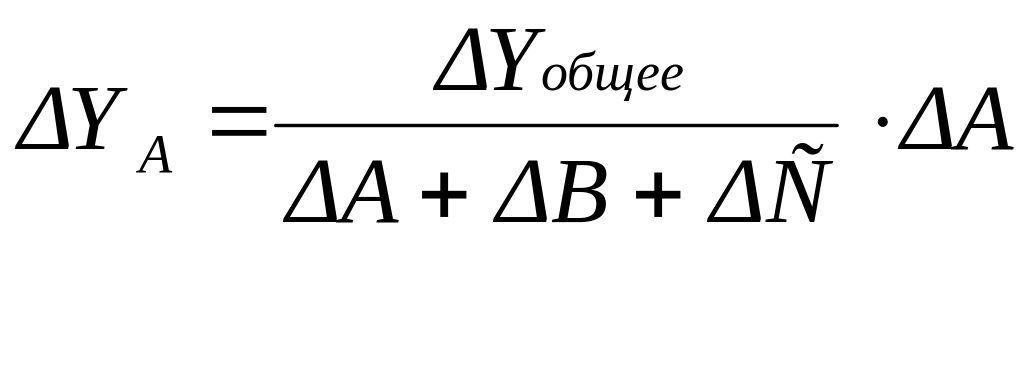
∆Y_В и ∆Y_С рассчитываются аналогично.

Согласно приему долевого участия определяется объём долевого участия как удельный вес изменения исследуемого факторного показателя в общем изменении всех факторов.

Пример. У = А·В·С. А, В, С – факторы, У – результативный показатель.

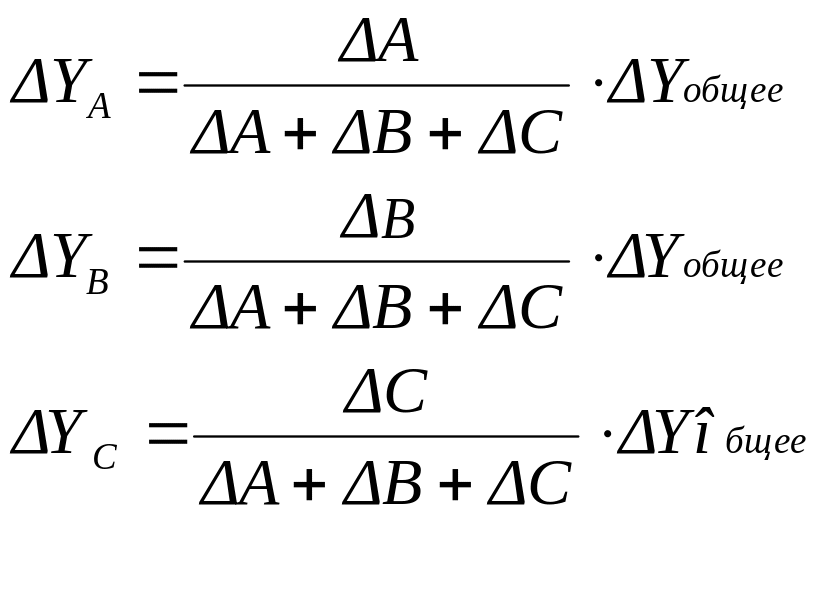
коэффициент долевого участия

В кратных моделях влияние фактора, стоящего в знаменателе, по указанным методам не всегда возможно определить объективно. Указанные приёмы, как правило, в смешанных моделях применяются в сочетании.

7. Применение приема логарифмирования и интегрального метода

Широкое использование математических методов является важным направлением совершенствования экономического анализа, повышает эффективность анализа хозяйственной деятельности предприятия. Это достигается за счет сокращения сроков проведения анализа, более точной оценки влияния факторов на результаты коммерческой деятельности, замены приближенных или упрощенных расчетов более точными вычислениями, постановки и решения новых задач анализа.

Логарифмический метод. Применяется для мультипликативных моделей. Его суть состоит в том, что достигается логарифмически пропорциональное распределение остатка по двум искомым факторам. В этом случае не требуется установления очередности действия факторов. Математически этот метод описывается следующим образом.

Факторную систему z = xy можно представить в виде: lgz = lgx + lgy.

Тогда Δz = lgz₁ – lgz₀ = (lgx₁ – lgx₀) + (lgy₁ – lgy₀), или

,

где lgz₁ = lgx₁ + lgy₁; lgz₀ = lgx₀ + lgy₀.

Разделив обе части формулы на lg и умножив на Δz, получим:

(1)

или

где

или .

Выражение (1) для z представляет собой не что иное, как его логарифмическое распределение по двум искомым факторам. Особенность логарифмического метода разложения состоит в том, что он позволяет определить безостаточное влияние не только двух, но и многих изолированных факторов на изменение результативного показателя, не требуя установления очередности действия. Формулу (1) для z можно записать иначе:

Δ z = Δ z_x+ Δ z_y = Δ zK_x+ Δ zK_y, (2)

где

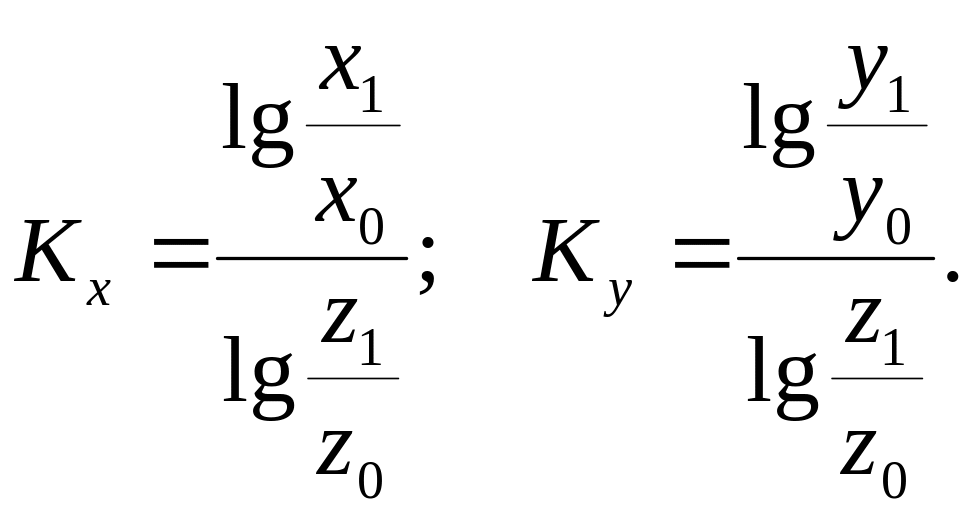
В таком виде формула (2) в настоящее время используется как классическая, описывающая логарифмический метод анализа. Из этой формулы следует, что общее приращение результативного показателя распределяется по факторам, пропорционально отношению логарифмов факторных индексов к логарифму результативного показателя. При этом не имеет значения, какой логарифм используется (натуральный или десятичный).

Интегральный метод. Как и приёмы пропорционального деления, долевого участия, логарифмирования в отличие от приёмов элиминирования, интегральный метод учитывает совместное влияние нескольких факторов. Он применим как к мультипликативным, так и к кратным, смешанным моделям. Расчёт влияния факторов в интегральном методе основан на теории дифференциального исчисления, в частности использовании функции нескольких переменных и определении её частных производных.

Использование этого метода позволяет получать более точные результаты по сравнению с приемами цепных подстановок и его разновидностями. При применении этого метода результаты анализа не зависят от порядка расположения факторов в модели, а дополнительный прирост результативного показателя, который образовался от взаимодействия факторов, раскладывается между ними пропорционально изолированному их воздействию на результативный показатель.

Двухфакторная модель F=XY

Трехфакторная модель F=XYZ