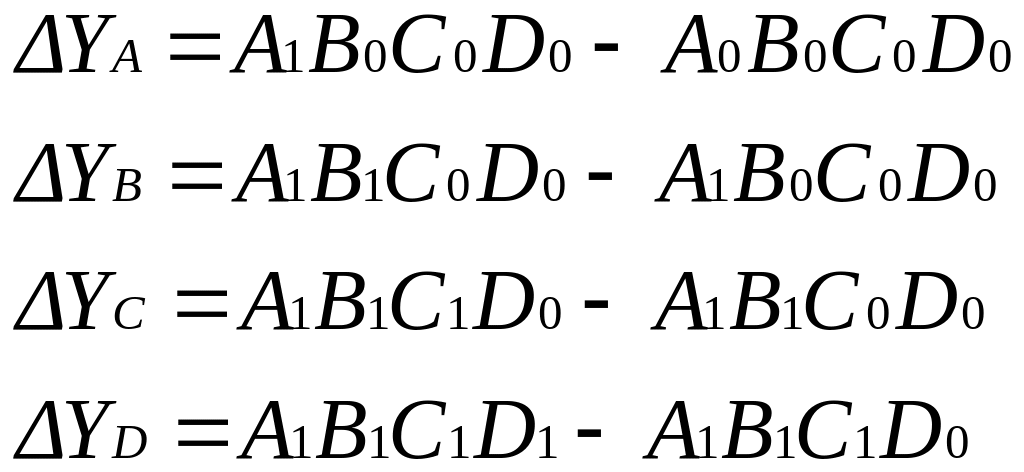- •2. Роль экономического анализа в управлении предприятием
- •3. Информационное обеспечение ахд и организация аналитической работы
- •Метод анализа хозяйственной деятельности
- •К) характеристика документов, которыми лучше всего оформлять результаты анализа;
- •Применение приема средних величин и графического способа в ахд
- •Применение приема относительных величин и балансового метода в ахд Прием относительных величин
- •Балансовый метод Это специальный прием сопоставления взаимосвязанных показателей хозяйственной деятельности с целью выяснения и измерения их взаимного влияния, а также подсчета резервов.
- •Виды факторных моделей
- •Применение приема цепных подстановок, абсолютных и относительных разниц в ахд
- •При использовании приема цепных подстановок важно обеспечить строгую последовательность подстановки. В первую очередь выявляется влияние количественных показателей, а затем – качественных.
- •7. Применение приема логарифмирования и интегрального метода
- •8. Метод корреляционно-регрессионного анализа
- •Тема 3. Анализ основных средств, материальных и трудовых ресурсов промышленности
- •2. Анализ использования производственного оборудования и мощности предприятия
- •3. Анализ обеспеченности предприятия материальными ресурсами
- •4. Анализ обеспеченности предприятия трудовыми ресурсами
- •5. Анализ использования рабочего времени
- •6. Анализ оплаты труда
- •2. Анализ эффективности использования материальных ресурсов
- •3. Анализ производительности труда
- •4. Анализ трудоёмкости продукции
- •5. Сущность хозяйственных резервов и методика их подсчета
- •Тема 5. Анализ себестоимости продукции в промышленности
- •1. Анализ структуры и динамики себестоимости продукции
- •2. Анализ прямых материальных и трудовых затрат
- •3. Анализ косвенных затрат
- •4. Анализ затрат на рубль товарной продукции
- •2. Анализ выполнения плана производства и реализации продукции
- •3. Анализ производства продукции по структуре, ассортименту, качеству и ритмичности
- •1. Анализ состава и динамики прибыли
- •2. Анализ рентабельности деятельности
- •3. Анализ распределения и использования прибыли
- •4. Анализ соотношения «издержки-объем-прибыль»
- •Безубыточный объем реализации в натуральных единицах рассчитывается по формуле:
- •Тема 8. Анализ финансового положения предприятия
- •1. Анализ внеоборотных активов предприятия
- •Анализ источников внеоборотных активов предприятия
- •3. Анализ оборотных активов предприятия
- •4. Анализ источников оборотных активов предприятия
- •5. Анализ платёжеспособности предприятия
- •6. Анализ деловой активности предприятия
- •7. Анализ финансовой устойчивости предприятия
- •Тема 9. Анализ хозяйственной деятельности в торговле
- •1. Анализ выполнения плана и динамики розничного товарооборота. Анализ товарооборота по составу, ассортименту и структуре
- •2. Анализ обеспеченности товарными ресурсами и эффективности их использования
- •3. Анализ качества торгового обслуживания
- •4. Анализ издержек обращения в торговле
- •5. Анализ валового дохода торгового предприятия
- •6. Анализ прибыли и рентабельности в торговле
- •7. Особенности анализа хозяйственной деятельности предприятий оптовой торговли
- •Тема 10. Анализ хозяйственной деятельности предприятий питания
- •1. Анализ товарооборота предприятий
- •2. Анализ выпуска собственной продукции
- •3. Анализ издержек в общественном питании
- •4. Анализ финансовых результатов деятельности предприятий питания
- •2. Анализ выполнения плана строительно-монтажных работ (смр) и продолжительности строительства
- •Тема 12. Анализ хозяйственной деятельности
- •2. Анализ технического обслуживания и ремонта подвижного состава. Анализ расхода топлива и материальных ресурсов на автотранспортных предприятиях
- •2. Анализ использования земельного фонда
Виды факторных моделей
Количественное измерение влияния факторов в детерминированном анализе производится на основе факторной модели. Факторная модель представляет собой функциональную зависимость результативного показателя от факторных.
В АХД выделяются следующие виды моделей:
Аддитивная, в которой результативный показатель представляется в виде суммы факторных показателей
![]()
Пример: Балансовая прибыль = прибыль от реализации + прибыль от прочей реализации + прибыль от внереализационной деятельности;
Капитал предприятия = собственный капитал + долгосрочные обязательства + краткосрочные обязательства;
Мультипликативная, в которой результативный показатель
представляется в виде произведения факторных показателей
![]()
Пример: Выручка от реализации = количество произведённой продукциицена
Среднегодовая выручка 1 работника = средняя выработка за 1 часколичество часов в сменудней в году = среднедневная выручкаколичество дней
Кратная (отношение факторных показателей)
![]()
Пример:
Рентабельность=![]()
Фондоотдача
ОПС=![]()
4. Смешанная (комбинированная). Результативный показатель представляется одновременно в виде суммы, отношения или произведения факторных показателей
![]()
![]()
![]()
Пример:
Рентабельность =
![]() ,
где
,
где
МЗ - материальные затраты
РОТ - расходы на оплату труда
ОТЧ - отчисления на соц. нужды
ПРЗ - прочие затраты.
Построить факторную модель - представить результативный показатель в виде алгебраической суммы, произведения или частного факторных показателей, оказывающих на результативный непосредственное влияние и находящихся с ним в функциональной связи.
Применение приема цепных подстановок, абсолютных и относительных разниц в ахд
Существуют две группы методов измерения влияния факторов на результативный показатель.
Приёмы элиминирования:
приём цепных подстановок;
приём абсолютных разниц;
приём относительных разниц;
индексный метод.
Математические приёмы:
интегральный приём;
приём логарифмирования;
приём долевого участия и пропорционального деления.
В основе приёмов элиминирования лежит нейтрализация (устранение) влияния всех факторов, кроме одного, влиянию которого даётся оценка. Условие обособленности влияния факторов в приёмах элиминирования является недостатком этой группы методов, так как в хозяйственной жизни предприятия воздействие факторов является одновременным. При использовании приёмов элиминирования важно обеспечить правильность последовательности записи факторных показателей в модели, так как последовательность расчётов измерения влияния факторов определяется записью факторных показателей в модели.
Прием цепных подстановок. Его сущность заключается в последовательной замене буквенного значения факторного показателя на текущее значение. В результате замены рассчитываются условные значения результативного показателя, называемые цепными подстановками. Влияние факторов измеряется при этом как разность между одним условным значением результативного показателя (или его текущим значением) и другой цепной подстановкой (или базисным значением результативного показателя). Количество цепных подстановок на единицу меньше, чем количество факторов в модели. Преимуществом данного приёма является тот факт, что он применим ко всем видам моделей. Недостаток: большая длительность расчётов, чем при использовании приёмов абсолютных и относительных разниц.
Степень влияния того или иного фактора выявляется последовательным его вычитанием.
Пример. У = А·В·С·D.