1. Аксиомы статики.

1. Аксиома о равновесии двух сил: если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда, и только тогда, когда эти силы равны по величине, и направлены вдоль одной прямой в противоположные стороны.

2. Аксиома о добавлении или отбрасывании уравнений системы сил: если на твердое тело действует система сил, то можно добавить или отбросить уравновешенную систему сил, полученная после добавления или отбрасывания сила эквивалентна первоначальной.

3. Аксиома параллелограмма сил:  Две силы, приложенные к телу в одной точке, имеют равнодействующую, проходящую через эту точку и равную их геометрической сумме.

4. Аксиома о равенстве действия и противодействия: при всяком действии одного материального тела на другое имеет место такое же по величине, то противоположное по направлению - противодействие.

5. Аксиома о связях: эффект от действия связей такой же как от действия определенных дополнительных сил которые могут быть приложены к свободному телу вместо связей.

Аксиома отвердевания: равновесие мех. системы не нарушается от наложения новых систем сил.

2. Принцип освобождаемости от связей. Простейшие типы опор и их реакции. (шарнирно-неподвижная, шарнирно-подвижная опоры и жесткая заделка).

Принцип освобождаемости от связей: несвободное твердое тело можно рассматривать как свободное, если его мысленно освободить от связей, заменив их действие реакциями.

Шарнирно-неподвижная опора.

О

y

пора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.

A

x

 Шарнирно-подвижная опора допускает горизонтальное перемещение и не допускает вертикальное. Реакция направлена по нормали к опорной поверхности.

ж есткая заделка не допускает никакого перемещения детали. Реакцией такой опоры являются неизвестная по величине и направлению сила R_A  с углом  α (или X_A  и Y_A ) и момент Μ_A 

α

3. Система сходящихся сил, условия равновесия. (определение, условия равновесия в векторной и алгебраической формах).

Для равновесия сходящихся систем сил приложенных к твердому телу необходимо и достаточно чтобы равнодействующая или главный вектор были равны нулю.

1. г

   F2

   F3

   еометрическое условие равновесия: для равновесия системы сходящихся сил необходимо и достаточно чтобы силовой мнооугольник построенный из этих сил был замкнутым.

F1

F4

F5

Fn

2. Аналитическое условие равновесия: модуль главного вектора системы сил в общем случае можно определить по формуле:

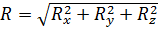
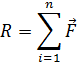
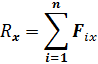
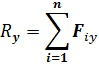
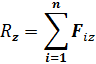
4. Момент силы относительно точки. (определение момента, понятие плеча силы, вычисление момента).

Моментом силы F относительно центра О называется приложенная к точке О вектор ( )(момента относительно точки О) равной векторному произведению вектора силы F на радиус вектора F.

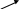
h

( h-расстояние от центра О до линии действия силы( плечо силы F))

Вектор (F) приложен в точке O и направлен перпендикулярно плоскости, проходящей через центр О и силу F.

Направлен вектор момента в ту сторону откуда откуда кратчайшее совмещение ОА с F происходит против хода часовой стрелки. Момент силы относительно точки характеризует вращательный эффект силы.

Св-ва момента силы:

1. Момент силы относительно центра не изменится при переносе точки силы вдоль линии ее действия.

2.момент силы относительно точки равно нулю в двух случаях:

1)когда сила равна нулю.

2)линия действия силы проходит через данную точку