19. Понятие вариации

Причиной вариации являются разные условия существования разных единиц совокупности.

Вариация — это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.

Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному соче¬таются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.

Поэтому возникает необходимость измерять вариацию при¬знака в совокупностях. Для этой цели в статистике применяют ряд обобщающих показателей.

К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение, коэффициент вариации.

20. Абсолютные и средние показатели вариации. Дисперсия альтернативного признака.

Абсолютные показатели:

1 ) Размах вариацииR. Размах вариации показывает лишь крайние  (min, max) отклонения признака от общей средней. Для анализа вариации необходим показатель, который отражает все колебания варьирующего признака и дает обобщенную характеристику.

2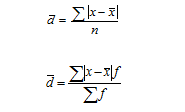 ) Среднее линейное отклонение — средняя арифметическая абсолютных значений отклонений (модуль отклонений) отдельных вариантов от их средней арифметической:

1. для несгруппированных данных (простое)

2. для сгруппированных данных (взвешенное)

3) Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средних величин. В зависимости от исходных данных вычисляется по формулам:

	для несгруппированных данных
	для сгруппированных данных

Расчет дисперсии может быть упрощен.

Cвойства дисперсии:

1. если все значения признака уменьшить или увеличить на одну и ту же постоянную величину А- дисперсия не изменится;

2. если все значения признака уменьшить или увеличить в одно и то же число раз (k раз), то дисперсия уменьшится или увеличится в k2 раз.

4) Среднее квадратическое отклонение измеряется в тех же едини­цах, что и варьирующий признак, и исчисляется путем извлече­ния квадратного корня из дисперсии:

	для не сгруппированных данных
	для сгруппированных данных

Среднее квадратическое отклонение, как и среднее линейное отклонение, показывает, на сколько в среднем отклоняются кон­кретные варианты признака от его среднего значения. Величина о часто используется в качестве единицы измерения отклонений от средней арифметической

Средние показатели

1)Коэффициент вариации – характеризует меру вариации значений признака вокруг средней величины. Дает относительную оценку вариации и получается путем сопоставления среднего линейного или среднего квадратического отклонения со средним уровнем явления, а результат выражается в процентах: Чем коэффициент меньше, тем однороднее совокупность и наоборот, чем больше тем неоднороднее.

Так как коэффициенты вариации дают относительную харак­теристику однородности явлений и процессов, они позволяют сравнивать степень вариации разных признаков.

Линейный коэффициент вариации	или
Коэффициент осциляции

Дисперсия альтернативного признака (если в статистической совокупности признак изменяется так, что имеются только два взаимно исключающих друг друга варианта, то такая изменчивость называется альтернативной) может быть вычислена по формуле: 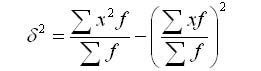Подставляя в данную формулу дисперсии q =1- р, получаем: Коэффициент роста K_i определяется как отношение данного уровня к предыдущему или базисному, показывает относительную скорость изменения ряда. Если коэффициент роста выражается в процентах, то его называют темпом роста.