2.7.2 Показательный закон распределения

Говорят, что случайная величина имеет показательное (экспоненциальное) распределение, т. е. , если она непрерывна, принимает только положительные значения и имеет функцию распределения

(2.7.2.1)

и, следовательно, функцию плотности распределения

(2.7.2.2)

где – единственный параметр показательного распределения, .

Из графика функции плотности распределения видно (рисунок 25, б), что случайная величина , имеющая показательное распределение, наиболее вероятно принимает малые положительные значения, менее вероятно – большие положительные значения.

а) б)

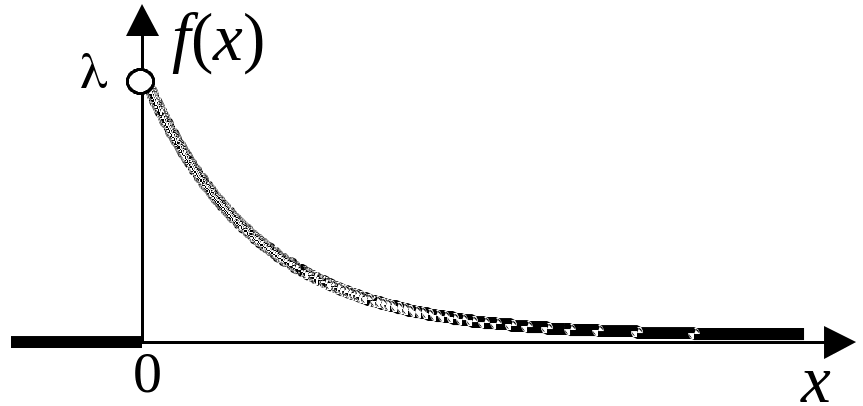
Рисунок 25 – Показательный закон распределения:

а – функция распределения F(x) случайной величины ;

б – функция плотности распределения f(x) случайной величины 

Основные числовые характеристики случайной величины , имеющей показательный закон распределения, определяются следующими выражениями:

(2.7.2.3)

Примерами случайных величин, имеющих показательный закон распределения, являются: время простоя вагона в ожидании ремонта, интервалы времени между поездами, прибывающими на станцию, время наработки на отказ электронных систем тепловоза и другие, поэтому показательное распределение имеет важное значение в теории надежности и теории массового обслуживания.

Случайная величина, распределенная по показательному закону, обладает важным свойством, называемым «отсутствием памяти».

Лемма об «отсутствии памяти» у показательного распределения. Пусть имеет показательное распределение с параметром (т. е. ). Тогда для любых и вероятность того, что величина примет значение меньше, чем при условии, что приняла значение не меньше, чем , равна безусловной вероятности того, что случайная величина примет значение меньшее, чем :

. (2.7.2.4)

Замечание – Если случайная величина – время до наступления некоторого события – имеет показательное распределение, то информация о том, что к моменту времени событие еще не наступило, не изменяет шансы на его наступление в дальнейшем. Этим свойством, называемым также отсутствием последействия, обладает только показательное распределение.

Пример 33

Время простоя вагона в ожидании ремонта является случайной величиной, распределенной по показательному закону с математическим ожиданием, равным 1,5 часа. Определить вероятность того, что в ожидании ремонта вагон простоит три часа.

Решение. Согласно условию, математическое ожидание случайной величины , обозначающей время простоя вагона в ожидании ремонта, равно 1,5. Учитывая, что для случайной величины, распределенной по показательному закону, , определяем значение параметра: . Функция плотности распределения данной случайной величины имеет вид

Определим вероятность простоя вагона в ожидании ремонта три часа:

Пример 34

Время безотказной работы электронного оборудования тепловоза является случайной величиной, распределенной по показательному закону. Определить вероятность безотказной работы оборудования в течение десяти часов эксплуатации, если среднее время безотказной работы по статистическим данным составляет 200 часов.

Решение. Согласно условию, математическое ожидание случайной величины , обозначающей время безотказной работы оборудования, равно 200. Учитывая, что для случайной величины, распределенной по показательному закону, , определяем значение параметра: . Функция плотности распределения данной случайной величины имеет вид

Определим вероятность безотказной работы оборудования в течение десяти часов эксплуатации:

Пример 35

Известно, что для некоторой сортировочной станции интервалы времени между поездами, прибывающими в разборку, представляют собой случайную величину , имеющую усечённое в точке показательное распределение:

Требуется: 1) вычислить параметр А и построить график функции плотности распределения ; 2) вычислить функцию распределения и построить её график; 3) вычислить числовые характеристики случайной величины (математическое ожидание, моду, медиану, дисперсию, среднее квадратическое отклонение); 4) вычислить вероятность того, что случайная величина примет значение в интервале (1; 2).

Решение. 1) Неизвестный параметр А плотности распределения вероятностей найдём из соотношения

.

Поскольку в данном примере плотность на равна нулю, то можно записать:

отсюда .

Следовательно, плотность распределения вероятностей имеет вид

Параметры распределения и имеют следующий смысл: – среднее число поездов, прибывающих на станцию в единицу времени; – минимальный допустимый интервал между последовательно прибывающими поездами.

Допустим поезда/ч, ч, тогда

График функции изображён на рисунке 26, а.

а) б)

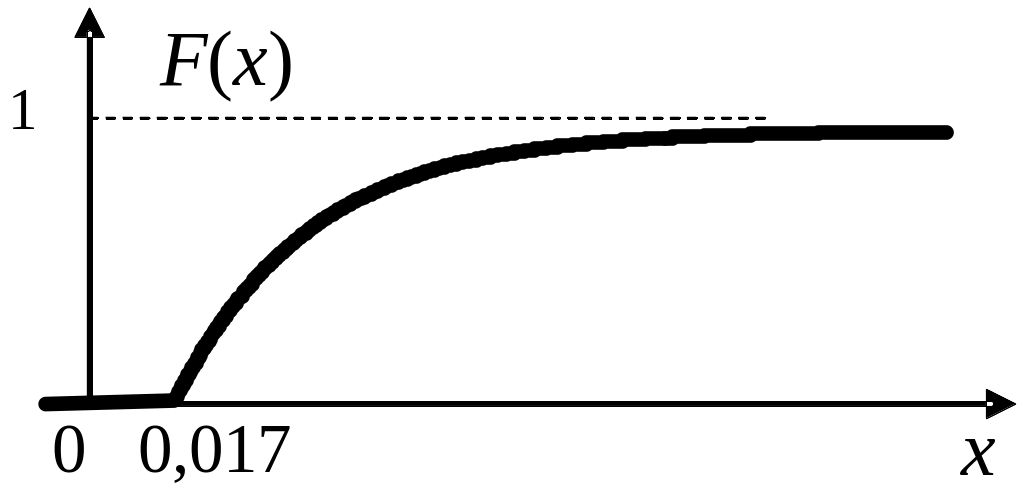
Рисунок 26 – Графики функций f(x) и F(x)

2) Вычислим функцию распределения :

при , ;

при ,

Следовательно,

График функции изображён на рисунке 26, б.

3) Числовые характеристики исследуемой случайной величины:

а) математическое ожидание

б) мода случайной величины равна 0,017 ч;

в) медиану найдём из уравнения :

г) дисперсия

д) среднее квадратическое отклонение

ч.

4) Вероятность того, что , вычислим по формуле

Вывод. Средний интервал времени между поездами, прибывающими на сортировочную станцию, равен 0,517 ч; наиболее вероятное значение интервала равно 0,017 ч; среднеквадратическое значение интервала между поездами равно 0,363 ч.