
Вопросы и шпоры к экзамену / Шпаргалки на 2 семестр
.doc|
Список экзаменационных вопросов по 2-й части сопротивления материалов для групп 2АС, 2ДВС. А. Основные.
|
1. Определение нормальных напряжений при косом изгибе.
Косым изгибом называется такое состояние бруса, при котором в поперечном сечении силовая плоскость не совпадает с главной плоскостью бруса. Основная идея определения напряжения состоит в разложении заданной по условию нагрузки на направления главных центральных осей опасного сечения (U, V) : Pv = Pcosα ; Pu = Psinα . Каждая из компонент нагрузки действует вдоль главных осей и поэтому вызывает прямой изгиб балки. Значит для каждой нагрузки можно рассчитать изгибающий момент в опасном сечении Mu , Mv , а затем найти σz : Mu = Pvl = Plcosα , Mv = Plsinα . Если действует только момент вокруг оси U, то σz(Mu) = (Mu / Ju )*V ; σz(Mv) = (Mv / Jv )*U ;
Применяя принцип суперпозиции получим окончательное выражение для σ при косом изгибе: σz(u,v) = (Mu / Ju )*V + (Mv / Jv)*U , где изгибающие моменты подставляются с учётом знаков. |
2. Определение положения нулевой линии при косом изгибе. Определение перемещений при косом изгибе.
Уравнение НЛ получим, приравняв к нулю выражение для σz(U,V), т.е. (Mu/Ju)*V + (Mv/Jv)*U = 0 ; V = - (Mv/Mu)*(Ju/Jv)*U ; V = - tgα*(Ju/Jv)*U tgβ = - tgα*(Ju/Jv).
Вычисление перемещений:
Vc1 = (Pv*L3)/(3EJк); Uc1 = (Pu*L3)/(3EJv); ∆C1 = √(Uc12 + Vc12);
Направление полного перемещения:
tgγ = Vc/Uc = [(PL3cosα)/(3EJu)]/[(PL3sinα)/(3EJv)] = (Jv/Ju)*ctgα ;
Но в уравнении НЛ : tgβ = - tgα Ju/Jv , => вектор полного перемещения при косом изгибе направлен по перпендикуляру к НЛ. |
3. Внецентренное действие продольной силы. Формула σ.
Перенесём Р в ЦТ поперечного сечения, присоединив два изгибающих момента, тогда N = P; Mu = P*Vp; Mv = P*Up. Нормальные напряжения в этом случае можно найти в результате суперпозиции решений для центрального растяжения и двух прямых изгибов, относительно U,V: σz(u,v) = N/F + (Mu/Ju)*V + (Mv/Jv)*U, где Mu и Mv берутся с учётом знака, т.е. положительные, если вызывают растяжение волокон I координатной четверти. U и V – координаты той точки на поперечном сечении, для которой вычисляется σ.
Если действуют несколько осевых нагрузок, то внутренние силы вычисляются по формулам с учётом знака: N = ∑Pi ; Mu = ∑Pi*Vpi ; Mv = ∑Pi*Upi. |
|||||||||
|
4. Нулевая линия при внецентренном действии продольной силы.
Для определения положения НЛ приравняем выражение σz(u,v) к 0: P/F + (P*Vp/Ju)*V + (P*Up/Jv)*U = 0 | *F/P 1 + (Vp*F/Ju)*V + (Up*F/Jv)*U = 0 iu = √(Ju/F); iv = √(Jv/F), тогда уравнение НЛ:
1 + (Vp/iu2)*V + (Up/iv2)*U = 0 Пусть V = 0, U = au , => au = - iv2/Up ; av = - iu2/Vp ;
НЛ делит поперечное сечение на 2 зоны – растянутую и сжатую. Приближая точку приложения силы к ЦТ можно вывести НЛ за пределы поперечного сечения (из формулы следует, что уменьшение координат Up,Vp даёт увеличение отрезков au,av по абсолютной величине). Если сила приложена в ЦТ , то НЛ -> ∞. |
5. Ядро сечения и его построение.
Вокруг ЦТ поперечного сечения существует область (ядро сечения), обладающая следующим свойством : Приложение продольной силы внутри ядра сечения или на его границе вызывает нормальные напряжения одного знака по всему поперечному сечению.
Для того, чтобы найти границу ядра сечения, нужно последовательно рассмотреть такие положения НЛ, при которых они касаются контура поперечного сечения не менее чем в 2 точках. Найдём координаты точки, в которой должна быть приложена сила: UpI = - iv2 / auI ; VpI = - iu2 / avI; Аналогично рассмотрим ещё две линии, совпадающие с границами контура сечения не меньше, чем в 2 точках. Соединив точки 1,2,3 получим ядро сечения. |
7. Доказательство теоремы о взаимности возможных работ.
направлении 2. δ21 – перемещение в направлении 2 от силы, приложенной в направлении 1.
Рассмотрим 2 точки и перемещения в них. Пусть вначале приложена сила F1, а затем F2. Потом, вначале приложена сила F2, а затем F1. Приравняем деформации: A1 = ½*F1*δ1 + ½ F2*δ2 + F1*δ12 A2 = ½ F2*δ2 + ½ F1*δ1 + F2*δ21 Тогда F1δ12 = F2δ21 , т.е. Работа первой силы на перемещении, вызванном второй силой, равна работе второй силы на перемещении, вызванном первой силой.
8. Вывод формулы о взаимности перемещений.
При F1=F2 из теоремы взаимности работ следует теорема взаимности перемещений, т.е. δij = δji . Перемещение в направлении i от единичной силы, приложенной в направлении j, равно перемещению в направлении j от единичной силы, приложенной в направлении i. |
9-1. Напряж. Состояние в точке. Определение главных напряжений и гл. площадок в общем случае нагружения.
Р Рассмотрим равновесие элементарного кубика: ∑Miz=0 : - τxydydzdx + τyxdxdzdy = 0 , => τxy = τyx . Аналогично для остальных координат. Т.о. в общем случае напряж. состояния в произвольных площадках для произв. точки выполняется закон парности τ .
Напряжённое состояние в общем случае принято задавать матрицей.
Главными называются площадки, на которых отсутствуют касательные напряжения. Если в выбранной точке вырезать элементарный кубик с главными площадками, то на них останутся только нормальные напряжения, которые называются главными. Н |
|||||||||
|
9-2. Пусть эта грань отсекает от исходного кубика элементарный тетраэдр. Пусть положение нормали к главной площадке в исходной системе к-нат определяется направляющими косинусами (L, m, n). Рассмотрим равновесие элементарного тетраэдра: dFx = dF·L : L = cos(ν^x); dFy = dF·m : m = cos(ν^y); dFz = dF·n : n = cos(ν^z); ∑Fix = 0 : σν·dF·L – σx·dF·L – τyx·dF·m – τzx·dF·n = 0 Аналогично для остальных координат, => (σx - σν)L + τyx·m + τzx·n = 0; τxy·L + (σy - σν)m + τzy·n = 0; L2 + m2 + n2 =1, => τxz·L + τyz·m + (σz - σν)n = 0; Определитель равен нулю, тогда σν3 – Y1σν2 + Y2σν – Y3 = 0, где Y1-3 – коэффициенты кубического уравнения – инварианты напряжённого состояния в точке. Y1 = σx + σy + σz ; Y2 = σxσy + σyσz + σzσx – τxy2 – τyz2 – τzx2 ;
Y3 = После нахождения Y1-3 решают кубическое уравнение и находят σ1-3 , учитывая что индексы ставятся в соответствии с условием : σ1≥σ2≥σ3
σx τyx τzx τxy σy τzy τxz τyz σz |
1 На передней и задней грани отсутствуют τ, => эти площадки главные. Кроме этого на них отсутствуют и σ, значит одно из трёх главных напряжений равно 0 и имеется двухосное напряжённое состояние. Возьмём прямоугольную систему координат, в которой по оси X – σ, а по оси Y – τ. Тогда каждой площадке (τ, σ) можно поставить в соответствие изображающую точку.
Соединяем К1 и К2 – центр круга Мора.
Построим полюс P. Плавно изменяя угол α можно добиться такого состояния, когда точка пересечения окажется на оси абсцисс, => τα = 0 ; значит эти точки являются изображением точек главных площадок. Если min > 0, то σmin = σII ; σIII = 0. Если min < 0, то σmin = σIII ; σII = 0. Если из Р провести луч через верхнюю и нижнюю точки круга, то получим изображение точки для площадки с max и min τ, т.е.
|
1
П Пусть действует только σ1, => ε1 = σ1/E ; Вдоль первого главного напряжения деформацию найдём из закона Гука: ε2 = -μ ε1 = -μ σ1/E ; ε3 = -μ ε1 = -μ σ1/E ;
ε2 = σ2/E ; ε1 = -μ ε2 = -μ σ2/E ;
ε3 = -μ ε2 = -μ σ2/E ; ε3 = σ3/E ; ε1 = -μ ε3 = -μ σ3/E ;
ε2 = -μ ε3 = -μ σ3/E ;
Если теперь сложить деформации по первому, второму и третьему гл. напр., то : ε1 = 1/E[σ1 – μ(σ2 + σ3)] ; ε2 = 1/E[σ2 – μ(σ1 + σ3)] ; ε3 = 1/E[σ3 – μ(σ1 + σ2)] ; (Обобщённый закон Гука для сложного напряжённого состояния). Если напряжённое состояние в точке задано не в главной площадке, то обобщённый закон Гука будет состоять из 6 уравнений: εx = 1/E[σx – μ(σy + σz)] ; εy = 1/E[σy – μ(σx + σz)] ; εz = 1/E[σz – μ(σx + σy)] ; для сдвиговой деформации: γxy = τxy /G ; γyz = τyz /G ; γzx = τzx /G . Все эти соотношения справедливы только для упругих деформаций изотропного иатериала.
|
12. Потенциальная энергия деформации для трёхосного напряженного состояния. Для трёхосного напряжённого состояния, используя принцип суперпозиции получим: U = ½σ1·ε1 + ½σ2·ε2 + ½σ3·ε3 Выразив деформации из обобщённого закона Гука, получим: U = [σ12 + σ22 + σ32 - 2μ(σ1 σ2 + σ2 σ3 + σ3 σ1)]/2E ; Любое напряжённое состояние всегда можно представить в виде следующей суммы:
σ1 Тогда U = Uо + Uф ; найдём эти слагаемые:
Uo = [σо2 + σо2 + σо2 - 2μ(σо2 + σо2 + σо2)]/2E = 3(1 - 2μ) σо2 /2Е ;
εv = ∆V/V0 = ε1ф + ε2ф + ε3ф = 0 (во втором напряжённом состоянии нет изменения объёма)
σ1ф = σ1 - σо ; σ2ф = σ2 - σо ; σ3ф = σ3 - σо ; => σ1ф – μ(σ2ф + σ3ф) + σ2ф - μ(σ1ф + σ3ф) + σ3ф - μ(σ1ф + σ2ф) = 0 ; После преобразования получим: σо = (σ1 + σ2 + σ3)/3 , и, подставив в формулу U0 :
U0 = (1 - 2μ) (σ1 + σ2 + σ3)2 /6E ;
Uф = U - U0 , тогда Uф = (1 + μ)[( σ1 - σ2)2 + (σ2 - σ3)2 + (σ3 - σ1)2]/6E |
|||||||||
|
13. Энергетическая теория прочности.
Два напряженных состояния называются равноопасными, если при одновременном увеличении всех компонент этих напряжённых состояний в n раз, разрушение (текучесть) наступает одновременно. Т.о. можно каждому сложному напряжённому состоянию поставить в соответствие равноопасное одноосное напряжение. Нормальное напряжение в этом фиктивном равноопасном напряжении называется эквивалентным напряжением. Переход от сложного напряженного состояния к эквивалентному напряжённому состоянию выполняют с помощью гипотез прочности. Энергетическая теория прочности.
Два напряжённых
состояния равноопасны, если у них
совпадают значения плотностей
потенциальных энергий изменения форм.
Т.о. если потенциальная энергия
изменения формы достигает некоторого
критического значения, материал
конструкции разрушается или «течёт»,
согласно IV
теории прочности.
Используя это
выражение найдём потенциальную энергию
изменения формы для фиктивного …
В частности для упрощенного плоского напряжённого состояния:
Эта гипотеза учитывает все главные напряжения и подходит для большинства материалов, одинаково работающих на растяжение и сжатие. Недостаток этой гипотезы в том, что она плохо подходит для материалов различно работающих на растяжение/сжатие. В этих случаях применяют теорию прочности Мора. |
14. Гипотеза максимальных касательных напряжений.
Два напряжённых состояния называются равноопасными, если у них совпадают значения max касательных напряжений, т.о., согласно этой теории, ответственность за разрушение лежит на τmax, т.е. они являются критериями разрушения или появления текучести.
Недостаток – неучёт второго главного напряжения. Упрощённое плоское состояние:
Е
Найдём главные напряжения: σ1 = σ2/2 + √[(σ2/2)2 + τ2] ; σ2 = 0 ; σ3 = σ2/2 - √[(σ2/2)2 + τ2] , => σэквIII = σ1 – σ3 = √( σz2 + 4τ2), т.е для вала с круглым попер. сечением:
Этот метод нельзя применять для прямоугольного и тонкостенного замкнутого сечения. |
15. Гипотеза Мора Гипотезы, указывающие признаки равноопасности (критерии эквивалентности) различных напряжённых состояний, называются гипотезами прочности.
Конструкция будет достаточно прочной, если точки с координатами (σ1 , σ3) попадут в заштрихованную область.
=> σ1 – kσ3 ≤ [σ]p Если материал одинаково работает на растяжение и сжатие, то k=1 и мы переходим к гипотезе τmax |
16. Расчёт на прочность стержней прямоугольного поперечного сечения при действующих: N, Qx,y , Mx,y , Mz .
Сложение двух изгибающих моментов не имеет смысла, т.к. суммарный изгибающий момент будет действовать вокруг оси, которая не является главной центральной осью, поэтому рассмотрим действие изгибающих моментов по отдельности, сначала вокруг оси Х, потом У.
Для сравнения различных сложных напряжённых состояний необходимо рассчитать в каждом случае σэкв:
Условие прочности: σэквmax ≤ [σ] |
|||||||||
|
1
Пусть балка нагружена произвольной системой внешних сил. Пусть нужно в точке К по направлению I-I найти перемещение.
Основные допущения:
Пусть под действием силы Р балка получает перемещение:
«К» - указывает точку, в которой ищем перемещение; «Р» - указывает на причину;
Сила Р на перемещении ∆АР возрастает линейно: АI = 1/2P·∆AP ; При статическом нагру
Ж
г Снимем силу Р и приложим в точке К по направлению I-I фиктивную силу Ф. По аналогии для работы:
|
17-2.
( Работа за II , III нагружение будет равна: А= 1/2Р·∆Ар +1/2Ф·∆Кф + ∆Кр·Ф Изгибающий момент в балке к концу третьего нагружения: Мх(р+ф) = Мхр + Мхф ; Потенциальная энергия:
A = U ,=>
|
17-3. Правило Верещагина.
Определённый интеграл от произведения двух функций, из которых одна линейна, а вторая произвольна, равен произведению площади графика произвольной функции на взятую под её Ц.Т. ординату графика линейной функции. Каждое из слагаемых, входящих в интеграл Мора, равно произведению площади ω нелинейной эпюры изгибающих моментов на ординату ηе линейной эпюры под Ц.Т. нелинейной, делённому на жёсткость сечения (EJx) данного участка балки. |
18. Основы расчёта статически неопределимых систем методом сил. Канонические уравнения.
Метод сил заключается в том, что заданная статически неопределимая система освобождается от дополнительных связей как внешних, так взаимных, а их действие заменяется силами и моментами. Значения этих сил и моментов подбираются так, чтобы перемещения соответствовали тем ограничениям, которые накладываются на систему отброшенными связями.
(Заданная система)
Эквивалентная система – получается из основной путём приложения всех внешних нагрузок и неизвестных реакций связей. Приравнивая к 0 перемещения в направлениях 1 и 2 -> δ1 = δ11X1 + δ12X2 + δ1F = 0 ; δ2 = δ21X1 + δ22X2 + δ2F = 0 , где δ21 – перемещение в направлении 2 от действия единичной силы 1. Эти уравнения называются каноническими. Их число равно степени статической неопределимости системы.
|
|||||||||
|
19. Расчёт симметричных рамных конструкций по методу сил. Разложение нагрузки на симметричную и кососимметричную.
Симметричная Несимметричная нагрузка нагрузка У симметричной рамы в плоскости симметрии при симметричной внешней нагрузке обращаются в ноль кососимметричные силовые факторы, а при кососимметричной внешней нагрузке – симметричные силовые факторы. Коэффициенты канонического уравнения, у которого один индекс принадлежит симметричному, а другой кососимметричному фактору обращаются в ноль, т.к. в симметричной раме не возникает взаимных кососимметричных перемещений под действием симметричных нагрузок и наоборот. Эти условия сохраняют силу не только для плоских, но и для пространственных рам при любой степени статической неопределимости. |
20. Расчёт многопролётных балок (статически неопределимая система).
Д После построения эпюр и нахождения коэффициентов канонических уравнений мы получим систему уравнений трёхдиагональной структуры. Диагональные матрицы или таблицы получаются для систем, имеющих однотипные, повторяющиеся элементы (пролёты балки).
4X1 + X2 + 0 + … = -M (1) X1 + 4X2 + X3 + … = 0 0 + X2 + 4X3 + X4 + … = 0 0 + 0 + X3 + 4X4 + X5 + … = 0
Пусть Xi = Aa1i + Ba2i , подставив в (1) -> A + B = M Перепишем последнее уравнение системы в виде: Xn-2 + 4Xn-1 + Xn – Xn = 0 , => Aa1n + Ba2n = 0, тогда
|
21-1. Устойчивость сжатых стержней. Вывод формулы Эйлера для стержня с шарнирно опёртыми концами.
Устойчивость – способность сжатого стержня сохранять прямолинейную форму после снятия малоотклоняющих нагрузок.
Будем считать, что прогибы V(z) малы, а материал стержня следует закону Гука. Функция прогиба V(z) определяется в следующей системе координат: начало в Ц.Т. поперечного сечения, ось z – по оси бруса, ось Х – ось минимальной жёсткости (вокруг неё изгиб). Предположим, что изогнутая ось лежит в области положительных прогибов: VII = Mx(z)/EJx ; Mx(z) = -P·V(z); VII + (P/EJx)V = 0; VII + α2V = 0 , где α2 = P/EJx . Решение уравнения будет иметь вид: V(z) = c1·sin α·z + c2cos α·z ; Составим два граничных условия для определения неизвестных: Z = 0 , V(0) = 0 ,=> c2 = 0 V(z) = c1sin α·z ; z = L ; V(L) = 0 ,=> c1sin α·L = 0 Если предположить, что С1 = 0 , то мы получим функцию V(z) тождественно равную 0 для любых Z и α. Это соответствует прямолинейной форме равновесий, => C1 ≠ 0 (т.к. мы изучаем отклонённую форму). Тогда: sin αL = 0 ; αL = πn , n = 1,2 … ; α = πn/L , значит α2 = π2n2/L2 .
Приравнивая
правые части выражений α2
->
Тогда минимально возможная сила при которой существует отклонённая форма равновесия: n = 1, Pn = π2EJmin / L2 (Формула Эйлера). Когда сила Р ≥ Ркрит стержень переходит в новое отклонённое состояние, которое бывает устойчиво. Если Р < Ркрит , то устойчивой будет прямолинейная форма равновесия. Переход к отклонённой форме равновесия ещё не означает разрушение конструкции. |
21-2.
Для случаев закрепления стержня, отличных от рассмотренного, получим аналогичную формулу: Pпр = π2EJmin / (μL)2 , где Lпр = μL (приведённая длина), μ – коэффициент приведения длины; Т.о. для вычисления Рпр надо стержень с заданным закреплением концов «привести» к стержню с шарнирным закреплением, но другой длины. μ приблизительно можно найти как величину обратно пропорциональную количеству полупериодов синусоиды, которую можно приложить на изогнутой оси стержня с заданным креплением концов.
|
|||||||||
|
22. Гибкость стержня. Пределы применимости формулы Эйлера. Предельная гибкость.
Обозначим λ2 = (μL/imin)2 – гибкость, т.о. это отклонение приведённой длины μL к min радиусу поперечного сечения стержня. λ = μL/imin ; σпр = π2E/λ2 .
При уменьшении λ напряжения обычно растут и достигают предела пропорциональности. Если напряжения > σпр , то материал уже не подчиняется закону Гука и применять формулу Эйлера нельзя. Чтобы найти λ0, при котором ещё применима формула Эйлера:
Если λ > λ0 , то стержень большой гибкости и для него имеет место упругий продольный изгиб, т.е. после снятия Р = Рпр стержень вернётся в исходное прямолинейное состояние. Предельная гибкость зависит только от физико-механических свойств материала стержня и не зависит от его размеров (λ0 – const). Формула Эйлера применима лишь тогда, когда λ ≥ λ0 . |
23. Продольный изгиб за пределом упругости. Построение графика критических напряжений.
При λ < λ0 в материалах появляются пластические деформации и зависимость критических напряжений от гибкости не подчиняется гиперболе Эйлера. Любая стойка теряет несущую способность при достижении σтс . По мере увеличения гибкости ограничивающая по направлению кривая является нисходящей и сливается с гиперболой Эйлера. Если стержень очень короткий, то имеет место простое сжатие без потери устойчивости (λ < 50). Если 50 ≤ λ ≤ 100, то имеет место неупругий продольный изгиб и σпр приближенно можно найти по формуле Ясинского: σпр = a – bλ , где a и b – const. [кг/см2] Для Стали 3 : а = 3100 ; b = 11,4. |
24. Продольно-поперечный изгиб. Точное и приближённое решение.
Продольно-поперечный изгиб – вид нагружения прямого стержня продольной силой и системой поперечных сил. Составим дифференциальное уравнение упругой линии: EJyII = -Py + Mп , где Mп – момент поперечных сил, Py – момент продольной силы; Тогда: yII + k2y = Mп/EJ Решив это дифференциальное уравнение найдём:
Выведем приближённую формулу для Mmax: EJyII = Mп – Py (дифференциальное уравнение упругой линии); При отсутствии продольной силы: EJyпII = Mп , тогда EJyII = EJyпII – Py , => y = f·sin(πz/L); yп = fп·sin(πz/L) Тогда: EJ·f·π2/L2 = EJ·fп·π2/L2 +P·f ,=> f = fп / (1 – P/Pпр) ;
Предполагая изгибающие моменты пропорциональные прогибам, -> M = Mп / (1 – P/Pпр) |
25. Краевое напряжение при продольно-поперечном изгибе.
Расчёт напряжений в наиболее удалённых от нейтральной оси волокнах проводится по сжатым волокнам (краевые напряжения).
|σzmax| = Mx/Wx + N/F ; |
|||||||||
|
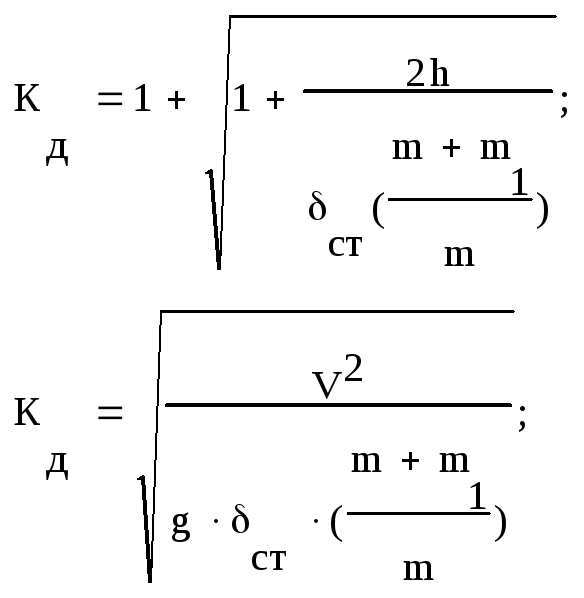
26, 27. Вывод Kд для горизонтального и вертикального удара.
h – высота с которой движется груз; G – масса груза; δдsinα – на эту величину груз ещё сместится вниз; δG – деформация от веса (статическая);
Энергия поднятого груза полностью переходит в потенциальную энергию деформации. Составим баланс энергий: G(h + δдsinα) = ½Fд·δд = ½KдG·Kд ·δG = ½ Kд2·G·δG ; Kд2 - 2 Kдsinα – 2h/ δG = 0, тогда
Из условия равновесия потенциальных энергий до и после удара: mgh = (m1 + m2)gh1 , => h1 = mh/(m + m1) , тогда:
|
2
Совокупность всех возможных напряжений фиксированной точки вала за один период нагружения называется циклом. σm = (σmax + σmin)/2 – среднее напряжение цикла; σa = (σmax - σmin)/2 – амплитудное напряжение цикла; Коэффициент асимметрии цикла: r = σmin/σmax. Различают: симметричный, асимметричный, пульсационный цикл.
При циклически изменяющихся напряжениях разрушение конструкции наступает при напряжениях значительно меньших предела прочности и текучести. Т.о. под усталостью понимается процесс постепенного накопления повреждений в материале под действием переменных во времени напряжений, которые приводят к зарождению и росту трещин вплоть до разрушения конструкции. Для экспериментального изучения усталостных свойств материалов проводят испытания образцов на различных уровнях max напряжения цикла. Обычно испытывают симметричным циклом в условиях изгиба, растяжения, сжатия и кручения. По результатам испытаний строят зависимость max напряжений цикла от числа циклов до разрушения.
Для расчёта на прочность в условиях переменных напряжений вводят понятие коэффициента запаса по пределу выносливости: nσ = σ-1 / σa (при симметричном цикле) |
29. Факторы, влияющие на усталостную прочность.
Если деталь содержит концентр. напр., то предел выносливости её будет заметно ниже: Kσ = σ-1 / σ-1K > 1 (эффективный к-нт концентрации) Величина Kσ зависит от геометрии детали, вида нагружения и материала. Хрупкие материалы более чувствительны к концентрации напряжения. Kσ можно приблизительно рассчитать: αТ = σmax / σномин. , где σmax – max значение нормального напряжения в зоне концентрации при статическом нагружении. σномин – нормальное напряжение концентрации в зоне нагружения, рассчитанное по формулам сопромата. q: 0,6-0,8 – углеродистые стали;0,2 – низкоуглеродистые; 0,9 – титановые. Kσ = 1 + q(αT – 1), q = (Kσ – 1)/(αT – 1);
εп = σ-1пов-ти / σ-1 , < 1 (может быть > 1) Коррозия ухудшает состояние поверхности.
εМ = σ-1d / σ-1 , < 1 Т.о. суммируя все факторы можно записать выражение коэффициента запаса:
|
30. Диаграмма предельных амплитуд. Определение коэффициента запаса при несимметричных циклах.
tgα = ψσ ; Простейший способ приближения диаграммы ПА состоит в замене диаграммы одной прямой, проходящей через крайние точки: nσ = OM1 / OK ; nσ = σ-1 / (σa + ψσ·σm) ; Если необходимо рассчитать nσ для детали при наличие концентратора с заданным состоянием поверхности и диаметром, то формула преобразуется по аналогии с симметричным циклом. Аппроксимация двумя прямыми:
Для аппроксимации 2 прямыми нужна ещё одна точка на диаграмме ПА. Через точку А и С можно провести прямую. 2 прямая строится из точки В под углом 45 к оси абсцисс. σmax = σв ; σm + σa = σв . Т.о. для всех точек на 2 прямой выполняется σm + σa = σв и если точка попадает на 2 прямую, то разрушение происходит мгновенно, менее чем за 1 цикл, => можно всё пространство под прямыми разделить на 2 зоны. Если точка в I зоне, то расчёт nσ делают по пределу выносливости (σ-1). Если точка попадает во II зону, то nσ находят из условия статического разрушения: nσ = σв / σmax = σв /(σm + σa). Если τ меняются циклически, то формула для nσ выглядит аналогично, только вместо σ – τ.
При одновременном
действии σ и τ применяется эмпирическая
формула Гаффа-Полларда:
|

 Изгибающий момент
положителен, если он вызывает растяжение
волокон в первой координатной четверти
(в осях U,
V)
опасного сечения.
Изгибающий момент
положителен, если он вызывает растяжение
волокон в первой координатной четверти
(в осях U,
V)
опасного сечения.



 Из уравнения
видно, что НЛ, в отличие от косого
изгиба, не проходит через ЦТ поперечного
сечения балки. В таком случае НЛ удобно
строить по отрезкам, кот она отсекает
на координатных осях U,V
- (au,
av).
Из уравнения
видно, что НЛ, в отличие от косого
изгиба, не проходит через ЦТ поперечного
сечения балки. В таком случае НЛ удобно
строить по отрезкам, кот она отсекает
на координатных осях U,V
- (au,
av).

 δ12
– перемещение в направлении 1 от силы,
приложенной в
δ12
– перемещение в направлении 1 от силы,
приложенной в
 ассмотрим
произвольную точку на произвольно
нагруженном теле. Вырежем в окрестности
этой точки бесконечно малый кубик и
приложим на его гранях все возможные
нормальные и касательные напряжения.
На невидимых гранях они будут направлены
в противоположную сторону.
ассмотрим
произвольную точку на произвольно
нагруженном теле. Вырежем в окрестности
этой точки бесконечно малый кубик и
приложим на его гранях все возможные
нормальные и касательные напряжения.
На невидимых гранях они будут направлены
в противоположную сторону.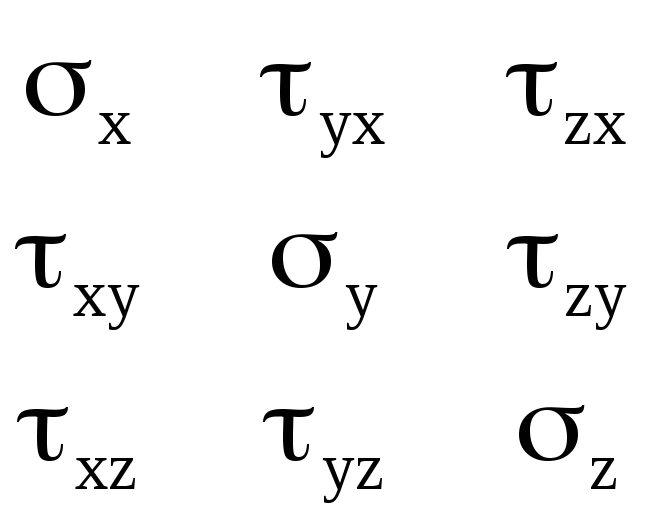
 айдём
величину главных напряжений σ1-3
, имея в качестве исходных данных
напряжения на произвольных площадках.
айдём
величину главных напряжений σ1-3
, имея в качестве исходных данных
напряжения на произвольных площадках. Представим,
что внутри исходного кубика есть
наклонная грань с нормалью ν и главным
напряжением σν.
Представим,
что внутри исходного кубика есть
наклонная грань с нормалью ν и главным
напряжением σν.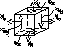 0.
Графическое определение главных
напряжений и положения главных площадок
для двухосного напряжённого состояния
(построение круга Мора).
0.
Графическое определение главных
напряжений и положения главных площадок
для двухосного напряжённого состояния
(построение круга Мора). Пусть σx
> σy
, τxy
> 0, => τyx
< 0, т.о. правой площадке соответствует
изображающая точка К1,
для верхней площадки К2
с коэффициентами (σy
, τyx).
Пусть σx
> σy
, τxy
> 0, => τyx
< 0, т.о. правой площадке соответствует
изображающая точка К1,
для верхней площадки К2
с коэффициентами (σy
, τyx). 1.
Обобщённый закон Гука.
1.
Обобщённый закон Гука. усть
напряжённое состояние в точке задано
в главных площадках, т.е. найдены
главные напряжения σ1-3.
Найдём соотношение между деформациями
ε1-3
с одной стороны и напряжениями σ1-3
, используя принцип суперпозиции.
усть
напряжённое состояние в точке задано
в главных площадках, т.е. найдены
главные напряжения σ1-3.
Найдём соотношение между деформациями
ε1-3
с одной стороны и напряжениями σ1-3
, используя принцип суперпозиции. = σ1об
+ σ1ф
; σ2
= σ1об
+ σ1ф
; σ2 = σ2об
+ σ2ф
; σ3
= σ2об
+ σ2ф
; σ3 = σ3об
+ σ3ф
;
= σ3об
+ σ3ф
;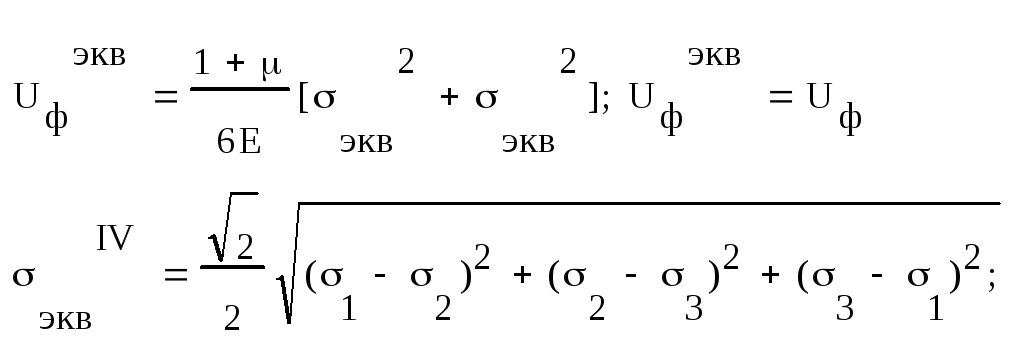
 сли
вал с круглым поперечным сечением
нагружен изгибающим моментом Mx
, My
, а также крутящим Mz
, то
изгибающие моменты можно векиорно
сложить между собой и относительно
наклонной оси, и мы получим прямой
изгиб. Кроме того действует крутящий
момент, тогда в точке наиболее удалённой
от оси U
вырежем кубик и рассмотрим нормальные
напряжения:
сли
вал с круглым поперечным сечением
нагружен изгибающим моментом Mx
, My
, а также крутящим Mz
, то
изгибающие моменты можно векиорно
сложить между собой и относительно
наклонной оси, и мы получим прямой
изгиб. Кроме того действует крутящий
момент, тогда в точке наиболее удалённой
от оси U
вырежем кубик и рассмотрим нормальные
напряжения: Гипотеза Мора
применяется для материалов различно
деформирующихся при растяжении и
сжатии.
Гипотеза Мора
применяется для материалов различно
деформирующихся при растяжении и
сжатии.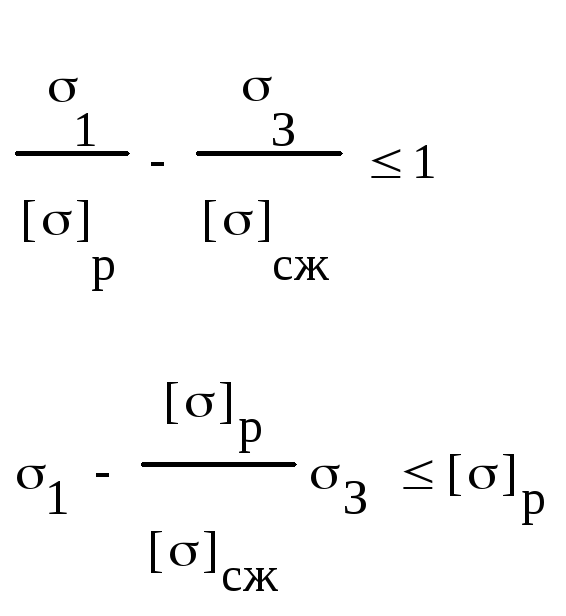


 7-1.
Вывод интеграла Мора.
7-1.
Вывод интеграла Мора. ении
вся эта работа пойдёт на накопление
потенциальной энергии деформации
балки.
ении
вся эта работа пойдёт на накопление
потенциальной энергии деформации
балки. де
Mxp
– функция изгибающего момента в балке
от действия заданной по условию
нагрузки Р.
де
Mxp
– функция изгибающего момента в балке
от действия заданной по условию
нагрузки Р.
 Не
снимая с балки силу Ф приложим в точке
А дополнительную силу Р)
Не
снимая с балки силу Ф приложим в точке
А дополнительную силу Р)



 Основная
система получается из заданной путём
устранения «лишних»
связей.
Основная
система получается из заданной путём
устранения «лишних»
связей.










 ля
многопролётной балки удобно образовывать
основную систему, врезая на опорах
шарниры и вводя в качестве неизвестных
опорные моменты.
ля
многопролётной балки удобно образовывать
основную систему, врезая на опорах
шарниры и вводя в качестве неизвестных
опорные моменты.
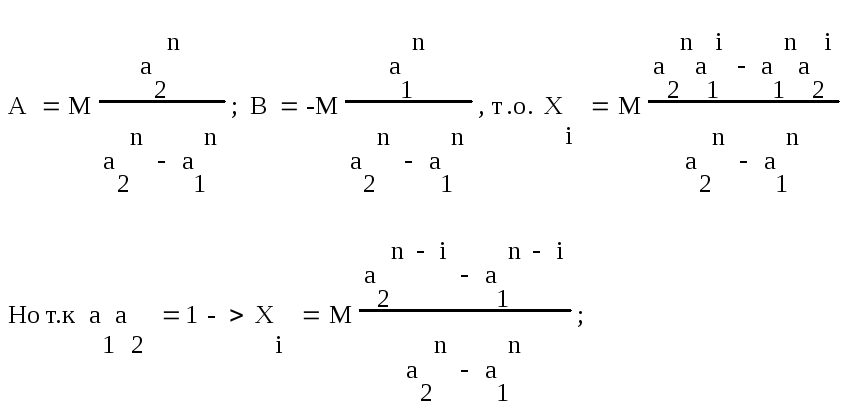
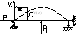 Найдём минимальное
возможное значение сжимающей силы P
= Pкрит.,
при котором возможно существование
отклонённой формы равновесия.
Найдём минимальное
возможное значение сжимающей силы P
= Pкрит.,
при котором возможно существование
отклонённой формы равновесия.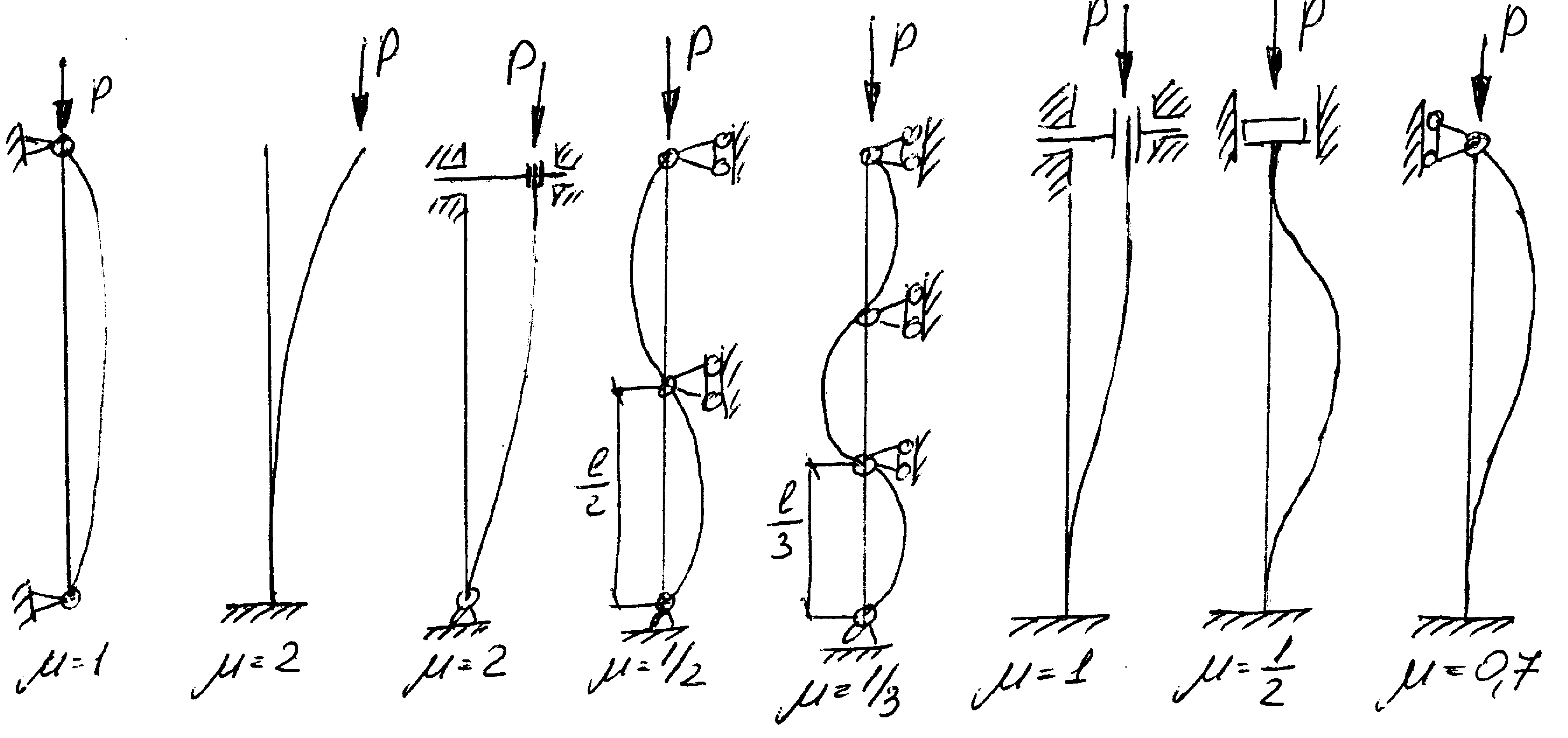




 Вертикальный
удар: α = 900;
Горизонтальный удар: α = 0 ;
Вертикальный
удар: α = 900;
Горизонтальный удар: α = 0 ;
 8.
Расчёты на прочность при циклически
изменяющихся напряжениях. Виды циклов.
8.
Расчёты на прочность при циклически
изменяющихся напряжениях. Виды циклов.
 Пределом
выносливости называется max
напряжение цикла, которое в состоянии
выдержать образец при циклическом
испытании неограниченным числом
циклов.
Пределом
выносливости называется max
напряжение цикла, которое в состоянии
выдержать образец при циклическом
испытании неограниченным числом
циклов.
