Теорема о трех перпендикулярах

Теорема 1. Теорема о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна её проекции, то она перпендикулярна и наклонной.

Теорема 2. Обратная теореме о трех перпендикулярах. Если прямая, проведенная на плоскости через основание наклонной, перпендикулярна наклонной, то она перпендикулярна и её проекции.

12) Угол между прямой и плоскостью — это угол между прямой и ее проекцией на данную плоскость.

Если прямая параллельна плоскости, значит, угол между прямой и плоскостью равен нулю.

Если прямая перпендикулярна плоскости, ее проекцией на плоскость окажется точка. Очевидно, в этом случае угол между прямой и плоскостью равен 90°.

Угол между плоскостями

Двугранный угол между плоскостями равен углу образованному нормальными векторами этих плоскостей.

Двугранный угол между плоскостями равен углу образованному прямыми l1 И

_l2, лежащими в соответствующих плоскостях и перпендикулярными линии пересечения плоскостей.

13) Вектор – направленный отрезок. Другими словами, вектором называется отрезок, для которого указано, какой из его концов является началом, а какой концом.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых. Если векторы   и   коллинеарны и их лучи сонаправлены, то векторы   и   называются сонаправленными.  Обозначаются  . Если векторы   и   коллинеарны, а их лучи не являются сонаправленными, то векторы   и   называются противоположно направленными.  Обозначаются  . Нулевой вектор условились считать сонаправленным с любым вектором. 

14)

14) Многогранник составленный из двух равных треугольников расположенных в параллельных плоскостях и n параллелограммов, называется Призмой.

Боковая поверхность прямой призмы равна произведению периметра основания на высоту призмы, т.е. на длину бокового ребра.  Доказательство  Боковые грани прямой призмы – прямоугольники. Основания этих прямоугольников являются сторонами многоугольника, лежащего в основании призмы, а высоты равны длине боковых ребер. Следовательно, боковая поверхность призмы равна 

15) боковая поверхность - Объединение боковых граней. Площадь боковой поверхности произвольной призмы S = P * l , где P - периметр перпендикулярного сечения, l - длина бокового ребра. Площадь боковой поверхности прямой призмы S = Pосн * l полная поверхность призмы Sполн. = Sбок + 2Sосн

16) Параллелепи́пед — призма, основанием которой служитпараллелограмм, или (равносильно) многогранник, у которого шесть граней и каждая из них — параллелограмм.

Свойства

• Параллелепипед симметричен относительно середины его диагонали.

• Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через середину его диагонали, делится ею пополам; в частности, все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

• Противолежащие грани параллелепипеда параллельны и равны.

• Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

17) Свойства диагоналей:     Все диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.

     Площадь поверхности: 

     Объем: 

     В частности, для куба 

18)Пирами́да— многогранник, основание которого — многоугольник, а остальные грани — треугольники, имеющие общую вершину.

Пирамида называется правильной, если основанием её является правильный многоугольник, а вершина проецируется в центр основания. Тогда она обладает такими свойствами:

• боковые ребра правильной пирамиды равны;

• в правильной пирамиде все боковые грани — конгруэнтные равнобедренные треугольники;

• в любую правильную пирамиду можно как вписать, так и описать около неё сферу;

• если центры вписанной и описанной сферы совпадают, то сумма плоских углов при вершине пирамиды равна 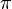 , а каждый из них соответственно  , где n — количество сторон многоугольника основания.

• площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

• Боковая поверхность правильной пирамиды равна произведению полупериметра основания на апофему

19.Правильная усеченная пирамида — это многогранник, у которого одна грань — основание пирамиды — правильный многоугольник, а остальные — боковые грани — равные треугольники с общей вершиной. Высота опускается в центр основания из вершины. Сечение параллельное основанию пирамиды делит пирамиду на две части. Часть пирамиды между ее основанием и этим сечением — это усеченная пирамида.

Боковая поверхность правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему:

20.Цили́ндр— геометрическое тело, ограниченное цилиндрической поверхностью и двумя параллельными плоскостями, пересекающими её. Цилиндрическая поверхность — поверхность, получаемая таким поступательным движением прямой (образующей) в пространстве, что выделенная точка образующей движется вдоль плоской кривой (направляющей). Часть поверхности цилиндра, ограниченная цилиндрической поверхностью называется боковой поверхностью цилиндра.Свойства и Элементы Круги называются основаниями цилиндра, а отрезки, соединяющие соответствующие точки окружностей кругов, − образующими цилиндра.  Так как параллельный перенос есть движение, то основания цилиндра равны.  Так как при параллельном переносе плоскость переходит в параллельную плоскость (или в себя), то у цилиндра основания лежат в параллельных плоскостях.  Так как при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние, то у цилиндра образующие параллельны и равны.  Поверхность цилиндра состоит из оснований и боковой поверхности. Боковая поверхность составлена из образующих.  Цилиндр называется прямым, если его образующие перпендикулярны плоскостям оснований.  Прямой цилиндр наглядно можно представить себе как геометрическое тело, которое описывает прямоугольник при вращении его около стороны как оси.

21.Ко́нус— тело в евклидовом пространстве, полученное объединением всех лучей, исходящих из одной точки (вершины конуса) и проходящих через плоскую поверхность

Свойства

• Если площадь основания конечна, то объём конуса также конечен и равен трети произведения высоты на площадь основания.

где S — площадь основания, H — высота. Таким образом, все конусы, опирающиеся на данное основание (конечной площади) и имеющие вершину, находящуюся на данной плоскости, параллельной основанию, имеют равный объём, поскольку их высоты равны.

• Центр тяжести любого конуса с конечным объёмом лежит на четверти высоты от основания.

• Телесный угол при вершине прямого кругового конуса равен

где   — угол раствора конуса.

22. Усеченным конусом- называют тело вращения, образованное вращением прямоугольной трапеции около боковой стороны, перпендикулярной основаниям.

Свойства:

Основание исходного конуса и круг, полученный в

сечении этого конуса плоскостью, называются основаниями усеченного конуса, а

отрезок, соединяющий их центры, — высотой усеченного конуса.

Часть конической поверхности, ограничивающая усеченный конус, называется его

боковой поверхностью, а отрезки образующих конической поверхности,

заключенные между основаниями, называются образующими усеченного конуса. Все

образующие усеченного конуса равны друг другу (докажите это самостоятельно).

Площадь боковой поверхности усеченного конуса равна произведению полусуммы

длин окружностей оснований на образующую:

Sбок = Пи (r + r1) l.

23.Шар – тело, ограниченное сферой.

Касательная плоскость к шару Плоскость, проходящая через точку A шаровой поверхности и перпендикулярная радиусу, проведенному в точку A, называется касательной плоскостью. Точка A называется точкой касания.  Теорема  Касательная плоскость имеет с шаром только одну общую точку – точку касания.   

24.Объем - это положительная величина, численное значение которой обладает следующими свойствами:

1)равные тела имеют равные объемы;

2)если тело составлено из нескольких тел , то его объем равен сумме объемов этих тел;

3)объем куба, ребро которого равно единице длины равен единице.

Объем параллелепипеда.

V=abc

25 Объём призмы

V = S_осн · h

26. Объём пирамиды

 

27. Объём усечённой пирамиды