6. Построение диаграммы условных напряжений

Диаграмма условных напряжений – это графическая зависимость условных напряжений σ_усл от относительных удлинений ε.

Она строится для того, чтобы исключить влияние масштабного фактора (масштабов по оси нагрузок и размеров образца), а также упругой деформации образца и деталей испытательной машины. На диаграмме мы имеем три точки: T – соответствует площадке текучести, напряжение равно физическому пределу текучести σ_T ; B – соответствует максимальной силе растяжения, когда условное напряжение равно временному сопротивлению σ_B; K – соответствует разрыву образца.

7. Расчет сопротивления металла пластической деформации.

1. Сопротивление металла пластической деформации - это напряжение при линейном напряженном состоянии, т.е. напряжение одноосного растяжения или сжатия в условиях пластической деформации, зависящее от температурно – скоростных условий деформирования. Сопротивление холодной пластической деформации обычно определяется при испытании на растяжении. Сопротивление горячей пластической деформации обычно определяется при испытании на сжатие.

В период равномерного удлинения имеет место однородное линейное напряженное состояние (рис 4) во всем объеме образца между метками, которые ограничивают расчетную линию.

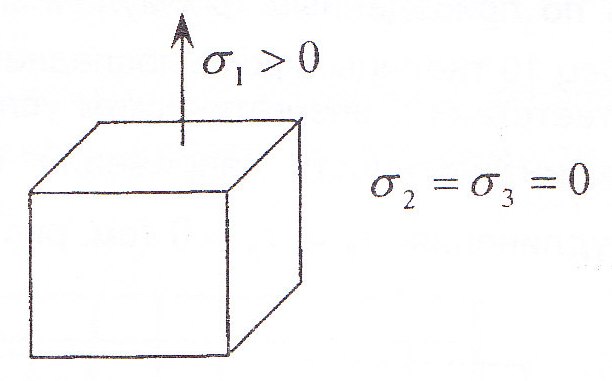
Рисунок 4. Схема главных нормальных напряжений в период равномерного удлинения

Тогда

Заменяя из условия постоянства объема , получим:

Еще раз подчеркнем, что эта формула справедлива только в период равномерного удлинения, включая точку В. В начале пластической деформации (точка Т)

Далее из-за упрочнения металла его сопротивление пластической деформации увеличивается. Поэтому иногда называют начальным пределом текучести, а – текущим пределом текучести, или напряжением текучести. В конце равномерного удлинения:

2. В период сосредоточенного удлинения коэффициент найдем по графику

Рисунок 5. График для определения поправочного

коэффициента по Г.А. Смирнову - Аляеву

Согласно энергетическому условию пластичности сопротивление металла пластической деформации в точке К:

8.Построение кривой упрочнения первого рода и её аппроксимация степенной зависимостью.

1. Кривые упрочнения необходимы для расчета процессов ОМД, т.к. по ним можно определить сопротивление металла пластической деформации.

Построить кривую упрочнения первого рода (вида) – графическую зависимость сопротивления металла пластической деформации σ_S от относительного удлинения ε

Показали на графике свойства кривой упрочнения: касательная, проведенная к кривой упрочнения первого рода в точке B, соответствующей началу образования шейки, отсекает на отрицательном направлении оси деформаций отрезок, численно равный 1, а на оси напряжений σ_S – отрезок, численно равный временному сопротивлению σ_B.

Эти свойства используются для линейной аппроксимации кривой упрочнения первого рода. В качестве аппроксимирующей прямой используется рассмотренная касательная. Тогда линейная аппроксимация (уравнение касательной) имеет вид

σ_{S =} σ_B + σ_B ε

2. Более точной является аппроксимация степенной зависимостью

σ_S = σ_T + Cεⁿ (*)

Для нахождения коэффициентов C и n необходимо иметь два уравнения. Первое уравнение получили, записав формулу для точки B:

σ_P = σ_T + C(ε_P)ⁿ=360,50+502,15*

Второе уравнение получим на основании свойства кривой упрочнения. Для точки B имеем dσ_S / dε = tgα, откуда

Cn(ε_P)^n-1 = σ_B

Решая полученную систему уравнений относительно C и n, найдём

n = σ_B ε_P / (σ_P - σ_T )= 709,24*0,31/(967,37-360,50)=0,362

C = (σ_P - σ_T ) / (ε_P)ⁿ= (967,37-360,50)/(0,31)^0,362=927,32

Построили по формуле (*) аппроксимирующую кривую. Для этого составили вспомогательную таблицу зависимости σ_S от ε. По формуле (*) вычислили соответствующие им значения σ_S. По семи точкам провели аппроксимирующую кривую.