4.Обработка диаграммы растяжения

1. В момент окончания периода равномерного удлинения образца и начала периода сосредоточенного удлинения, т.е. в момент начала образования на образце шейки, сила растяжения достигает максимального значения P_max .

Провели на диаграмме растяжения ось деформаций ∆l*m для определения абсолютных удлинений образца ∆l, мм, где m – масштаб диаграммы по оси деформаций.

Провели на диаграмме растяжения ось нагрузок P/n для определения сил растяжения образца P, Н, где n – масштаб диаграммы по оси нагрузок, Н/мм.

2. Определили масштаб диаграммы по оси деформаций. Для этого провели через точку К , соответствующую концу испытания (разрыву образца), прямую КК₁ , параллельно начальному прямолинейному участку диаграммы ОТ для исключения упругой деформации деталей испытательной машины и самого образца. Длина отрезка прямой ОК₁ в m раз больше остаточного (пластического) удлинения образца после разрыва

∆lк = lк - l₀ = 21 мм.

Тогда масштаб диаграммы растяжения по оси деформаций равен

m = OK₁ / ∆lк = 9,90

3. Определили масштаб диаграммы растяжения по оси нагрузок n. Для этого вначале определили положение на диаграмме растяжения точки B, соответствующей максимальной силе растяжения P_max. Рассчитали ∆lp – абсолютное остаточное равномерное удлинение образца к моменту образования на нем шейки:

∆lp = l₀[(d₀/dp)² – 1]= 50*[(10/8,73)² - 1]= 15,61 мм.

Эту формулу мы получили из условия постоянства объема. На оси деформаций отметили точку B₁, на расстоянии ∆lp*m, мм от начала отсчета точки О, ОВ₁=∆lp*m=52,12 мм. Провели прямую B₁B параллельно начальному прямолинейному участку диаграммы OT. Опустили из точки B на ось деформаций перпендикуляр BB₂. Тогда масштаб диаграммы растяжения по оси нагрузок равен:

n = P_max / BB₂= 516,40 H/мм.

4. Разделили диаграмму растяжения на участке TB, который соответствует периоду равномерного удлинения образца, на 5 частей. Провели через точки деления 1…4 прямые, параллельные начальному прямолинейному участку диаграммы OT. Получили на оси деформаций точки ∆l_₁*m…∆l₄*m, соответствующие абсолютным удлинениям образца ∆l_₁…∆l₄. Из точек 1…4, из точки K, а также из точки T, соответствующей началу текучести образца опустили на ось деформаций перпендикуляры для расчета соответствующих сил.

5. Составили таблицу по прилагаемой форме. Измерили в мм на диаграмме растяжения длины перпендикуляров, опущенных из точек T, 1…4, B, K на ось деформаций и записали их в столбец 2:

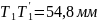
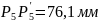
Умножили эти числа на масштаб n. Получили значения соответствующих сил в ньютонах и записали их в столбец 3:

6. Измерили в мм на оси деформаций диаграммы растяжения отрезки ∆l_₁*m…∆l₄*m и записали эти числа в столбец 4 таблицы:

∆l₁*m =20

∆l₂*m = 40

∆l₃*m = 60

∆l₄*m = 80

∆l₅*m =100

∆l₆*m =120

Разделив их на масштаб m, получили соответствующие значения остаточных (пластических) абсолютных удлинений образца ∆l в мм(столбец 5):

5. Определение механических свойств

1. Вычислили относительное удлинение образца

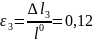
(столбец 6 таблицы). В конце равномерного удлинения (точка B)

ε_p = ∆l_p / l₀ = 0,31

Тогда относительное равномерное удлинение равно

δ_p = 100* ∆l_p / l₀=31 %

В конце испытания (точка K) получим относительное удлинение после разрыва

Δ₅ = 100* ∆l_k / l₀= 42 %,

где индекс “5” указывает на то, что испытывался короткий образец пятикратной длины (l₀ = 5d₀).

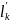Однако относительное удлинение в конце испытания ε_k рассчитывается по длине l_k, приведенной к поперечному сечению в месте разрыва. Из условия постоянства объема найдем, что = l₀F₀ / F_k =50*78,5/31,853= 123,22 мм. Тогда

ε_k = (l_k - l₀) / l₀=(123,22-50)/50=1,464 б/р

2. Вычислили относительное сужение поперечного сечения образца

q = (F₀ - F) / F₀

(столбец 7), где F, мм² – текущая площадь поперечного сечения образца. Поскольку текущий диаметр образца в процессе его растяжения не измерялся, вычислить площадь F через диаметр нельзя. Поэтому мы воспользовались условием постоянства объёма Fl = F₀l₀, где l = l₀ + ∆l – текущая расчетная длина образца. Тогда F = F₀l₀ / l и

q = (F₀ - F) / F₀ = (l - l₀) / l = ∆l / (l₀ + ∆l) = ε / (1 + ε)

В конце испытания (точка K) получили относительное сужение поперечного сечения после разрыва

Ψ = 100*(F₀ – F_K) / F₀ = 100q_k = 100ε_k / (1 + ε_k)=100*1,464/(1+1,464)=59,4 %.

3. Вычислили условные напряжения σ_усл = P / F₀, H/мм² (МПа)

(столбец 8). Условным напряжение называется потому, что текущая сила растяжения образца P относится к начальной площади его поперечного сечения F₀.

В начале испытания (точка T) получили физический предел текучести σ_T – наименьшее напряжение, при котором образец деформируется без заметного увеличения растягивающей нагрузки:

В конце равномерного удлинения образца (точка В) получим временное сопротивление (предел прочности) σ_B – напряжение, соответствующее наибольшей нагрузке P_max, предшествующей разрыву образца: