24. Алгоритм генерации отрезков (простой цда).

Общие требования к изображению отрезков:

1. Концы отрезков должны находиться в заданных точках

2. Отрезки должны выглядеть прямыми

3. Яркость вдоль отрезка должна быть постоянной и не зависеть от длины и наклона отрезка.

Концы отрезка расположены на пикселях лишь наиболее близких к требуемым позициям; только в частных случаях координаты концов отрезка будут совпадать с координатами пикселя.

Линия аппроксимируется набором пикселей и в итоге не имеет ничего общего с прямой линией. Только в частных случаях отрезок будет выглядеть прямым (строго вертикально ли строго горизонтально, в крайнем случае – под углом в 45 градусов).

Яркость страдает из-за того, что расстояние между пикселями неравномерное.

Ц ДА – цифровой дифференциальный анализатор.

Алгоритм позволяет растризовать отрезок, заданный двумя точками, используя при этом вычисления с вещественными числами (с плавающей точкой).

Простой ЦДА. В данном алгоритме одно из приращений, соответствующее более быстро меняющейся координате, приравнивается к 1, а приращение к другой координате определяется как соотношение высот. Например:

25. Алгоритм Брезенхема для генерации отрезков.

У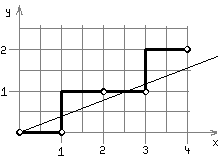 страняет недостатки алгоритмов ЦДА, а так же осуществляет приближение к идеальному отрезку, выбирая на каждом шаге пиксель, максимально приближенный к идеальной прямой.

Для принятия решения о том, куда заносить очередной пиксель, вводится величина отклонения E – точная позиция идеальной линии от середины между двумя возможными растровыми точками в направлении наименьшей относительной координаты.

Значение Е используется как критерий для выбора ближайшей растровой точки. Если E<0, то значение y округляется до последнего меньшего целочисленного значения (т.е. не меняется по сравнению с предыдущей точкой). Иначе y++.

На каждом шаге значение более быстро меняющейся координаты увеличивается на 1, по другой координате либо меняется, либо неизменно. Критерием этого изменения координаты является минимум расстояния до идеального отрезка.

Пример кода на С:

int x, y, Px, Py; double E = (Py/Px) – 0.5;

for(int i = 1; i <= Px; i++)

{ plot(x, y); if(E > 0) {y++; E--;} x++; E = E + (Py/Px); }

26. Проблема растровой развертки окружностей.

О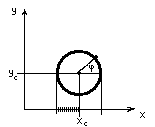 кружность – геометрическое место точек, удаленных на заданное расстояние R от центра (Xc, Yc).

Для любой точки (x,y) взаимосвязь с этим расстоянием R выражается через теорему Пифагора: . . Недостаток: большой объем вычислений, промежутки между положениями изображаемых пикселей будут неравновмерными.

27. Алгоритм Брезенхема для развертки окружностей.

При любом способе описания окружность можно сократить объем вычислений, если учесть симметрию окружности: ее форма одинакова во всех квадрантах, следовательно, если построить кривую в одном квадранте, с помощью аффинных преобразований можно получить всю окружность целиком. Так же можно использовать симметрию в октантах.

. Алгоритм пошагово генерирует очередные точки окружности, выбирая на каждом шаге для занесения пикселя точку , ближе к идеальной окружности так, чтобы .

Выбор ближайшей точки выполняется в помощью анализа значений управляющих переменных для вычисления которых не требуется вещественная арифметика. Для выбора очередной точки достаточно проанализировать знак

Dj = | (x + 1)² + y² - r² |

Dd = | (x + 1)² + (y + 1)² - r² |

Dv = | x² + (y + 1)² - r² |

Выбирается та точка, для которой D минимальна.