Алгоритм отсечения Коэна-Сазерленда.
Алгоритм Коэна — Сазерленда (англ. Cohen–Sutherland) — алгоритм отсечения отрезков, то есть алгоритм, позволяющий определить часть отрезка, которая пересекает прямоугольник. Был разработан Дэном Коэном и Айвеном Сазерлендом в Гарварде в 1966—1968 гг., и опубликован на конференции AFIPS в 1968.[1][2]
Алгоритм разделяет плоскость на 9 частей прямыми, которые образуют стороны прямоугольника. Каждой из 9 частей присваивается четырёхбитный код. Биты (от младшего до старшего) значат «левее», «правее», «ниже», «выше». Иными словами, у тех трёх частей плоскости, которые слева от прямоугольника, младший бит равен 1, и так далее.
Алгоритм определяет код конечных точек отрезка. Если оба кода равны нулю, то отрезок полностью находится в прямоугольнике. Если битовое И кодов не равно нулю, то отрезок не пересекает прямоугольник (так как это значит, что обе конечные точки отрезка находятся с одной стороны прямоугольника). В прочих случаях, алгоритм выбирает конечную точку, находящуюся вне прямоугольника, находит ближайшую к ней точку пересечения отрезка с одной из линий, образующей стороны прямоугольника, и использует эту точку пересечения как новую конечную точку отрезка. Укороченный отрезок снова пропускается через алгоритм.
Реализация алгоритма для трёхмерной модели идентична двумерной реализации, за исключением того, что вместо четырёхразрядного кода применяется шестиразрядный (дополнительные два бита глубины).
33.Синтез реалистических изображений. Расчет интенсивности при различных видах освещения.
Основной характеристикой света в компьютерной графике является яркость/интенсивность света. При расчетах освещенности грани применяют следующие типы освещения и отражения света от поверхности
Рассеянный источник света – интенсивность освещения граней считается постоянной в любой точке пространства. Вычисляется:
,
где
- интенсивность источника,
- коэффициент рассеянного отражения,
Диффузный источник света -
,
г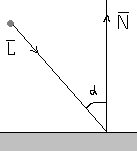
де
- интенсивность источника,
- коэффициент
диффузного отражения,
3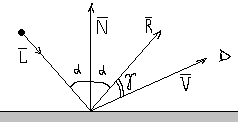
)
Зеркальный
– R
– вектор зеркально отраженного луча,
V
– определяет положение наблюдателя,
тогда:
,
где
- интенсивность источника,
-
зависит от отражающих свойств материала,
- коэффициент зеркального отражения,
- модель Фонга.
Интенсивность отраженного света
уменьшается обратно пропорционально
квадрату расстояния r
от объекта до наблюдателя:
,
R≥1
– определяет коэффициент проницаемости
среды.
В системе компьютерной визуализации так же учитываются такие свойства материалов, как преломление и прозрачность. Степень прозрачности может описываться с помощью константы, принимающей значение от 0 до 1, причем 1 будет соответствовать полной непрозрачности материала.
Классификация источников освещения. Проблема расчета затухания интенсивности (радиальное, угловое).
Любой объект, излучающий энергию, является источником света, дающим вклад в общее освещение сцены. Простейшая модель: точечный источник, имеющий 1 цвет. Параметры: координаты в пространстве и цвет. Использовать такую модель стоит, если источник пренебрежительно мал по отношению к сцене (например, сильно удален). Виды точечных источников:
Бесконечно удаленный источник света (солнце) – необходимо задать еще и направление света.
Радиальное
затухание интенсивности.
При распределении света от источника,
его интенсивность на некотором расстоянии
d
затухает с коэффициентом
.
Недостаток: такой коэффициент обычно
приводит к слишком большому разбросу
интенсивности для объекта, который
находится близко от источника. Для
получения более реалистичного изображения
затухание интенсивности можно моделировать
квадратичной функцией d(l)
с использованием коэффициентов:
;
здесь (1) – локальный источник света,
(2) – бесконечно удал
Угловое затухание
интенсивности
- показатель затухания
2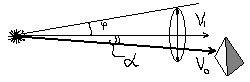
)
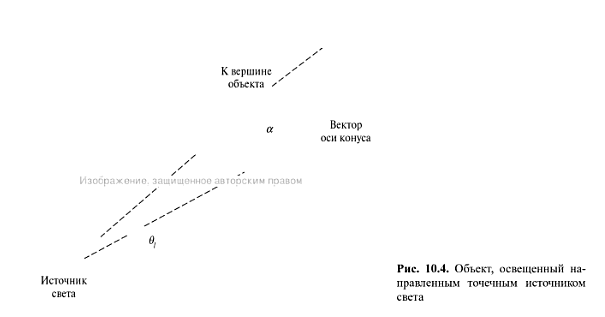
Направленный
источник света
(прожектор).
- единичный вектор в направлении светового
конуса,
- единичный вектор в направлении
освещенного объекта.
.
Если α>φ,
то объект не освещен данным источником.
Методы решения задачи закраски граней (постановка задачи, закраска с постоянной интенсивностью, интерполированное закрашивание).
Ключевая проблема - реалистическое представление освещенности.
Существует три основных способа закраски многоугольников: однотонная закраска, закраска с интерполяцией интенсивности и закраска с интерполяцией векторов нормали.
При однотонной закраске вычисляют один уровень интенсивности, который используется для закраски всего многоугольника. При этом предполагается, что:
Источник света расположен в бесконечности, поэтому произведение (
)
постоянно на всей полигональной грани.Наблюдатель находится в бесконечности, поэтому произведение (
)
постоянно на всей полигональной грани.Многоугольник представляет реальную моделируемую поверхность, а не является аппроксимацией криволинейной поверхности. Если какое-либо из первых двух предположений оказывается неприемлемым, можно воспользоваться усредненными значениями и , вычисленными, например, в центре многоугольника.
Последнее предположение в большинстве случаев не выполняется, но оказывает существенно большее влияние на получаемое изображение, чем два других. Влияние состоит в том, что каждая из видимых полигональных граней аппроксимированной поверхности хорошо отличима от других, поскольку интенсивность каждой из этих граней отличается от интенсивности соседних граней.
В методе закраски с интерполяцией интенсивности (метод Гуро) нормали в вершинах многоугольников вычисляются как результат усреднения нормалей ко всем полигональным граням, которым принадлежит данная вершина. Используя значения нормалей, вычисляют интенсивности в вершинах по той или иной модели освещения. Эти значения затем используются для билинейной интерполяции: для данной строки сканирования вначале находят значения интенсивностей на ребрах, а затем линейно интерполируют между ними при закраске вдоль строки.
В методе закраски с интерполяцией нормали (метод Фонга) значение нормали вдоль строки интерполируется между значениями нормалей на ребрах для данной строки. Значения нормалей на ребрах получается как результат интерполирования между вершинами. Значения же нормалей в вершинах являются результатом усреднения, как и выше рассмотренном методе. Значение нормали для каждого из пикселей строки используется для вычислений по той или иной модели освещения.