30. Основы фрактальной геометрии.

1875 г. – Вейерштрасс открыл непрерывную недифференцируемую функцию. Эффективная размерность не есть величина постоянная. Числовой результат ЭР всегда зависит от соотношения между объектом и наблюдателем, т. е. это субъективно относительная величина.

Возникновение фрактальной геометрии связано с именем Б. Мандельброта.

Фрактал – некое образование, самоподобное (самоафинное) в том или ином смысле.

Фракталом называется структура, состоящая их частей, которые в каком-либо смысле подобны целому.

Фрактальная геометрия – не евклидова.

Математически: - топологическая размерность; D – размерность Хауздорфа – определяет скорость изменения объекта в пространстве и времени (число элементов, покрытых окружностью радиусом ε)/(число, показывающее, сколько раз укладывается ε в единице длины). В евклидовой геометрии , в фрактальной - .

Фракталы делят на три больших класса:

1. Геометрические фракталы – в случае 2D-рисовки их получают с помощью некоторой ломаной линии, называемой генератором. За один шаг алгоритма каждый из сегментов, составляющих ломаную, заменяется на исходный генератор в соответствующем масштабе. В результате бесконечного повторения этой процедуры получается геометрический фрактал (кривая Коха, генератор Харта, канторовская пыль, салфетка Серпицкого).

2. Алгебраические фракталы – самая крупная группа, получают с помощью нелинейных процессов в n-мерных пространствах. Нелинейный итерационный процесс интерпретируется как динамическая система, используются понятия «фазовый портрет» и «аттрактор» (точка/область притяжения в фазовом пространстве). Такая система имеет несколько устойчивых состояний. То состояние, в котором оказалась динамическая система спустя некоторое количество времени (после некоторого числа итераций), зависит от начального состояния. Поэтому каждое устойчивое состояние (аттрактор) обладает некоторой областью начального состояния, из которого система с необходимостью попадет в рассматриваемый аттрактор. Т. о. все фазовое пространство разбивается на области притяжения аттракторов (множество Мандельброта, множество Жулиа [используются комплексные числа]).

3. Стохастические фракталы – фракталы, в математическое описание которых вводится вероятность фактора.

Операции с комплексными числами выглядят следующим образом.

Сложение: z = zl+z2, Re z = Re zl + Re z2, Im z = Im zl + Im z2

Вычитание: z = zl-z2, Re z = Re zl - Rez2, Im z = Im zl - Im z2

Умножение: z = zl • z2, Re z = Re zl • Re z2 - Im zl • Im z2, Im z = Re zl • Im z2 + Re z2 • Im zl

Деление: z = zl / z2, Re z = ( Re zl • Re z2 + Im zl • Im z2 ) / ( Re z2 • Re z2 + Im z2 • Im z2 ), Im z = ( Re z2 • Im zl - Re zl • Im z2 ) / ( Re z2 • Re z2 + Im z2 • Im z2 )

31. Алгоритмы отсечения. Постановка задачи.

Отсечение – процесс обнаружения и исключения из дальнейшего анализа элементов сцены, которые не попадают в видимую область, выражаемую на экране.

Объект, устанавливающий границы области отсечения, называется отсекателем, и в зависимости от размерности, области действия, сложности формы и средств реализации, отсекатели делятся на несколько видов:

1. Плоские 2D-отсекатели;

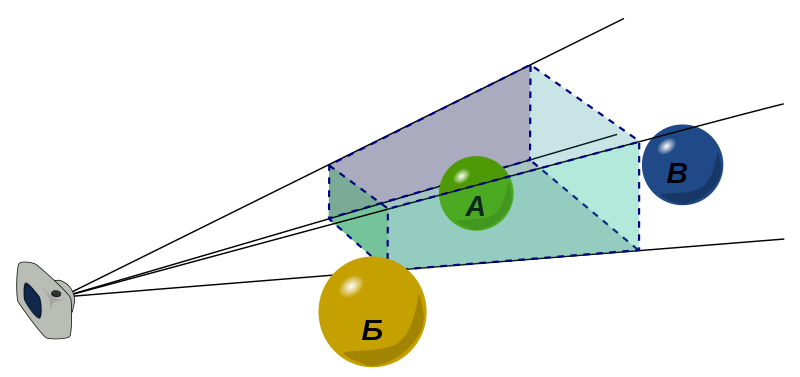
2. Объемные 3D-отсекатели: призма (при параллельном проецировании) или пирамида (при центральном проецировании);

3. Внешние отсекатели – отбрасываются элементы сцен, находящиеся вне отсекателя;

4. Внутренние отсекатели – отбрасываются те элементы сцен, которые расположены внутри отсекателя;

5. Регулярные – обычно прямоугольник или параллелепипед и ориентированы по координатным осям;

6. Нерегулярные – произвольной формы;

7. Аппаратные – реализованы аппаратными средствами видеопроцессора или центрального процессора. Обычно являются регулярными;

8. Программные – реализованы программными средствами.