Шпоры к экзамену

Теория вероятности. Предметом теории вероятности является анализ явлений, к-рые не всегда приводят к одним и тем же результатам, к-рые обладают статистической устойчивостью. Цель: научиться строить числовую меру объективной возможности событий. Математическая модель Т.В. Основой матем. модели явл-тся вероятностное пространство, к-рое обозначается (Ω,Cr,P).Ω(пространство элементарных событий),={ }. Вероятностное прост-во элем событий Ω-совокуп-ть всех различных исходов.ω-элементарное событие, задаёт один исход. На практике чаще интересуется составными событиями.

A={,,}

Диаграмма Венна 9удобно пользоваться для наглядности). Задание прост-ва элем.событий нашло более полно описывает изучаемое явление.Cr-вводит соотношение и тип операции над событием.Она определяет, насколько тонко различимы события.

P-это числовая мера объективной возможности наступления событий. Р(А)-ф-ция, определена на Ω(А), явл-тся числовой мерой, если не отриц.1)Р(А)0; 2)Р(Ω)=1нормирована; 3)для несовместных событий обладает след. св-вом: Р(

Алгебра событий.1)соотношение включений(что больше чего).Говорят, что множ-во В явл-тся частным случаем А,если А наступает всякий раз, когда наступает В.Ω-достоверное событие, если оно наступает в рез-те любого эксперимента (т.е. оно содержит в себе все элемен. события).ǿ-невозможное событие (не содержит ни одного элем.события).Операции над событиями.Объединение(сумма):А=ВUС=В+С(«или»). Сумма состоит из таких элем.событий, к-рые принадлежат или В, или С, т.е. эти элем. События принадлежат хотя бы одному множ-ву. Это соответствуетформальной логике операции «Или».Пересечение(произведение):в этом случае А состоит из таких элем. соб., к-рые входят и в первый вопрос и во второй.Взятие доплнений:-наз-тся противопол. соб., если оно состоит из элем. соб., к-рые не входят в А. А+=Ω

Дискретные вероят-ные прост-ва(счётные).

Ω ={,,…,}.;Классическая форма вер-ти: ;m-благоприятный исход;n-число испытаний.

=Следствия из аксиом.1:вер-ть против. соб. Р(А)=1-Р(А).2.Вер-ть невозможных событий.Р(ǿ)=0.3.Вер-ть частного случая, если АВР(А)Р(В).Теорема сложения:Р(А+В)=Р(А)+Р(В)-Р(АВ).Понятие о з-не больших чисел. Частотная интерпретация вер-ти.Опр.Отношение ) наз-тся условной вер-тью и оно равняется )=

Сл.1.Р(АВ)=Р(А))=Р(В)Р().Теорема:если )=Р(А),если усл.вер-ть равняется безусловной, то следует,что Р(АВ)=Р(А)Р(В). Мн-ва независимы, необходимы и достаточны, чтобы рав-ва выполнялись в ту и в другую сторону. Тогда св-во можно брать в качестве опред.независимости.

=Сл.2.Полная вер-ть. Декартовое разложение формулы:

Р(А)=

1.U =Ω

2.Hǿ

Множество ,удовлет. условию 1 и 2, наз-тся гипотезой.

Сл.3:теорема гипотез(формула Байеса).Эта теорема позволяет вводить новую инф-цию в алгоритм принятия решений и поэтапно уточнять решения. Теорема: предположим мы имеем гипотезу и априорные()вер-ти.2.пусть произошёл опыт, и наступило событие А().Тогда 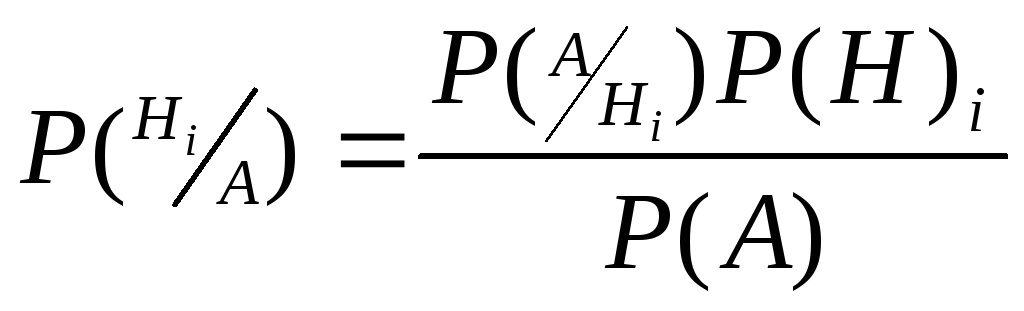Киберенетический смысл т.Байеса: если после появления события А производится ещё одно наблюдение, то усл.вер-ть может быть посчитана по след.форм-ле:

Декомпозиции(методы уравнений).

Схема Бернулли. Теорема Бернулли. Биномиальный з-н.

)=

Число слагаемых=числу способов,к-рые можно разместить k успехов в n испытаний.

Биномиальный з-н:

Задача Банаха. Дискретная модель Винерского процесса.

Цель:доказать в наглядной форме т. Бернулли. Условия: имеется 2 коробка спичек. Каждый раз, когда нужно достать спичку коробок вынимается случайно…может, когда вы вынимаете пустой коробок. Какова вер-ть того, что в другом коробке будет ровно r спичек.

Р(А)=

N=2m-r

Задача Буффон.

Цель:вычислить число π. Плоскость разделена на расстояния между линиями. На пл-ть на удачу бросается карандаш. Какова вер-ть того, что этот карандаш пересечёт одну из линий.

/e

ω=(x,φ),х-расстояние от середины полочки до ближайшей прямой,φ-угол между карандашом и параллельной линией.Опр-ть меру.u(Ω)=π,x=[0,],

φ=[0,π]

x=e/2∫sinφ,A:x

Случайные величины.Функции распределения случ.величины.Законы.Осн.идея-рез-том этих явлений могут быть представлены глобально-числовыми параметрами.Такими глобальными хар-ми явл-тся случ.величины.Сл. величина-это измеримая числовая ф-ция от событий.ξх.Сл.величины-греческие буквы(обозначение),значения сл.величин обозначаются англ.буквами.Сл.вел.кси наз-тся измеримой,если существует вер-ть попадания её в интервал,а для этого нужно, чтобы её первообр. являлось сл. событием,к-рое принадлежит сигма алгебре.{},

2)измеримость сл.величины,если сущест. вер-ть того,что кси принадлежит интервалу борельского множества.

Борель,,т.е. по сути существует вер-то того, что кси<x.F(x)такая вер-ть наз-тся ф-ция распределения.

Осн.св-ва ф-ции распределения(з-ны).

1.F(-)=0,F(+)=1,вер-ть меняется от 0 до 1.

2.,вер-ть того, что кси попадёт в интервал от a до b.

3.Ф-ция распределения монотонности неубывающая.

.Общий вид ф-ции распределения:

1)сл.величина значения не принимает (на гор. интервале);2)произошёл скачок в точке .

Дискретные сл.величины.Сл.величина кси наз-тся дискретной, если область её значений (х) не более чем счетно (можно сосчитать).

Ф-ция распределения дискретной сл.величины по опред. равняется вер-ть того,что ξ<х.

Примеры:1)равновероятные;2)биномиальный з-н;3)гипергеометрический з-н;4)геометрический з-н;5)распределение Пуассона.

Пуассоновские процессы,поля,пространства.Вер-ть обладает 3-мя св-ми(гипотезами):

1.Вер-ть каждого события зависит только от длины промежутка и не зависит от времени оси регистрации.Гипотеза стационарности.Кроме того, они не зависят между собой. Гипотеза линейности.Вер-ть того,что на интервале поступит хотя бы одно событие:

Сумма вер-тей,где λ-коэф-т

[t,t+Δt]=интервал интенсивности потока,λ-бесконечно малая по сравнению с интервалом Δt.3.Св-во ординарности.Т.е. вер-ть поступления на интервале Δt более одного события бесконечно мала.

-ур-ние баланса.Далее эта система с помощью преобразования Буреле, очень легко решается регулентно

Затем с помощью обратного преобразования Буреле получаем:

Сл.величина кси распределна по з-ну Пуассона с параметром а, если она принимает целочисленные значения с такой вер-тью:

З-н Пуассона.

Теорема Пуассона для редких событий.

Непрерывные сл.величины.Плотность вер-ти и её св-ва.Сл.величина кси наз-тся непрерывной, если существует некоторая ф-ция f(x),к-рая равна производной от ф-ции распределения.

,f(x)-плотность вероятностей.

Св-ва:1.f(x), производная, з-н распределения монотонно неубывающий.2.Интегральное св-во ф-ции распределения

3.Р(ξ=х)=0.4.

5.Вер-ть того.что сл.величина попадёт внутрь маленького интервала Δt,она

Важнейшие распределения непрерывного типа.

Равномерное распределние явл-тся моделью для игры с природой и в чпстности в качестве модели стратегии.Модель равномерного распределния.

Нормальный з-н или распределние Гаусса.

Показания к применению:если на исследуемые явления (рез-ом наблюдения) действует множество причин и каждая из них оказывает несущественное значение(т.е. нет доминирующих причин),то в рез-те сл.величина оказывается распределённой по нормальному зав-ну (или Гаусскому).Сл.величина кси распределна по нормальному з-ну,если её плотность вер-ти имеет следующий вид:

Случайные процессы ожидания.Модель показательного распределения. Экспоненциальный з-н.Для наглядности рассмотрим процесс ожидания чего-либо.Например,когда наступит вызов на техстанции. Рассматриваемый процесс обладает только одной особенностью независимо от того,как долго продолжается ожидание,вер-ть наступления события за малый промежуток времени пропорционально только длине этого промежутка.

Обозначим τ-сл.величина,характеризующая продолжительность времени ожидания.Наша цель:найти ф-цию распределения(з-н) для этой случ.величины.

,пр-сс закончиться до момента τ.-обратная случ.величине.

процесс не закончится к моменту t. Рассмотрим эту ф-цию в 3 момента времени:

вер-ть того,что процесс не закончится в последней точке.

плотность по определению равна производной от ф-ции

Замечание:только что полученный рез0т даёт возможность дать ещё обоснование опр-ния пуассоновских процессов.Пуассоновский пр-сс-это процесс,в к-ром расстояния между двумя соседними событиями есть непрерывная случ.величина,распределённая по экспоненциальному з-ну.

Числовые характеристики случайных величин.Глобальная логика нашего курса:1.Введённые ранне вер-ные прост-ва наиболее полно описывают изучаемые явления.2.Рассмотрение з-нов распределения-это некоторые суждения,т.к. мы требовали существование ф-ции распределения,одновременно указывая,какие значения принимает случ.величина и с какими вер-ми.3.Однако,на практике часто достаточно знать лишь числовые,интегральные характеристики случ.величин.1-ая хар-ка-МО.Суть:МО-это хар-ка положения,т.е. это такая величина,вокруг к-рой крутятся все значения случ.величин.МО для дискретных сл.величин.

Опр. Имеется случ.величина кси,тогда её МО есть сумма: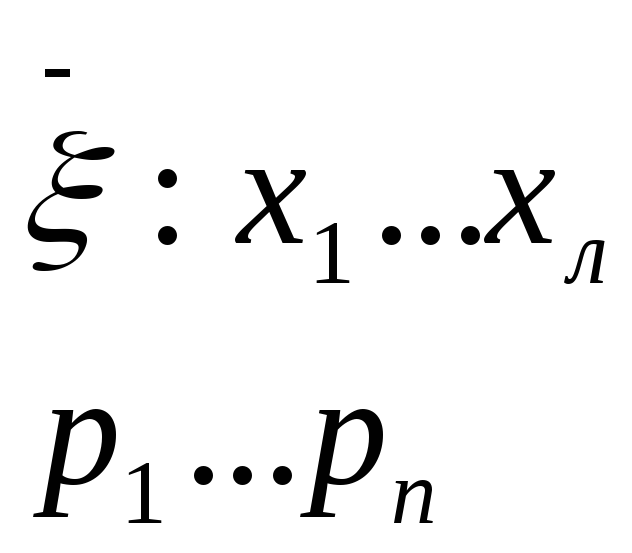

Опр.МО непрерывной сл.величинв:пусть существует некоторая ,тогда Мо есть интеграл

через интеграл Лимена.Учитывая,что f=производной от ф-ции распределения,получается:-интеграл Лебека.

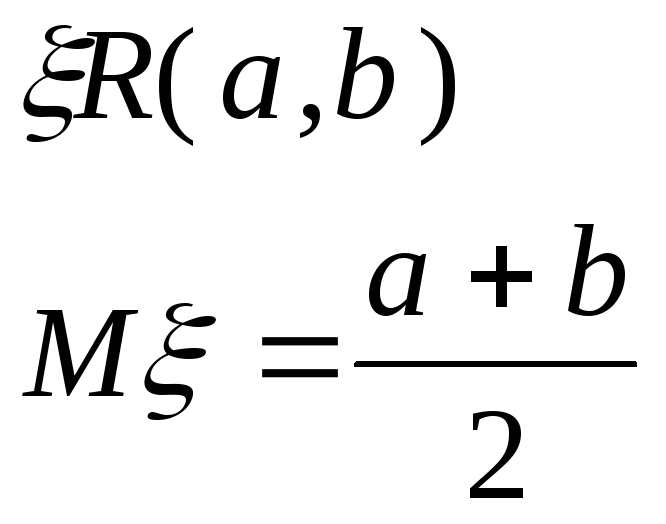
Определение условных МО.

Назовём условным МО случайной величины кси при условии B.

Основные теоремы о матем. ожиданиях.1.MC=C(неслуч.величина),т.к.С можно рассматривать как случайную величину (дискретную),принимающую одно значение СР=1. 2.МО произвед. на константу=…,потому что по опред. МО определяется суммой или интегралом-это линейные операции и константа выносится и за знак интеграла,и за знак суммы:;

3.МО суммы сл.величин явл-тся суммой математических ожиданий.Теорема №3 позволяет опр-ть Мо для схемы Бернулли.

Дисперсия случ.величины.По сути дисперсия явл-тся хар-кой рассеивания.

Дисперсией случ.величины-МО квадрата отклонения случ.величины от своего МО

1.Дисперсия константы.

DC=0

2.Дисперсия произведения случ.величины на неслуч.величину.

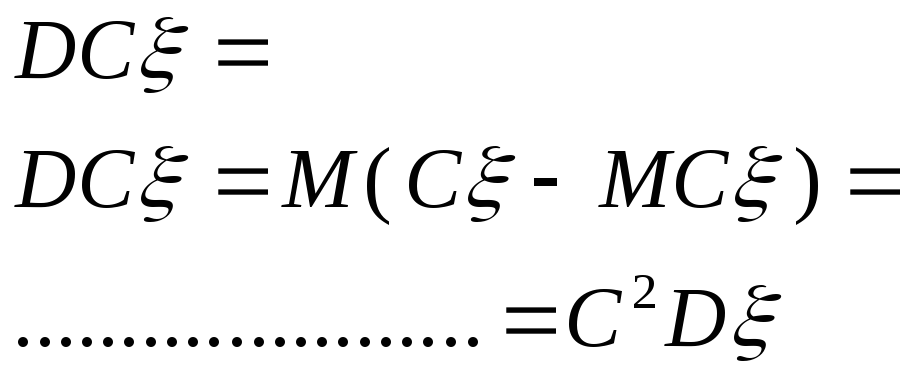
3.Дисперсия суммы двух неслучайных величин.

Внутри [ ] произведём перекомпановку.Если и n независимы,то коэф-т корреляции=0.Если коэф-т корреляции……………………………………….

В этом случае можно записать дисперсию разности в след.виде:

(-1)ушёл,т.к.квадрат. По определению,Мо квадрата случайной величины D для равномерной случ.величины на интервале q(0;1).

Ответ:

Дисперсия для случайной величины,распределённой по з-ну Бернулли:

Формулы:

В основном наиболее распрот-ные з-ны опр-тся двумя первыми моментами:1)МО;2)дисперсией.Однако,заметим,на практике существует случай,когда требуется введение и других числовых характеристик. Наиболее важными из них явл-тся моменты случ.величин.Моментом k-ого порядка случ.величины наз-тся МО

если а=0,то такой момент наз-тся начальный и обозначается .Если ,то такой момент-центральный,.Заметим,в начальный момент 1-ого порядка . Центральный момент 2-ого порядка-дисперсия

.Связь между моментами определяется по з-ну Бенома-Ньютона:

Прикладные св-ва моментов высших порядков.

-хар-ка ассиметрии (скошенности)

-хар-ка эксцесса (островершинности)