
- •Экзаменационные вопросы по курсу тммм
- •1) Основные понятия
- •2) Основные виды механизмов.
- •3) Кинематические цепи. Кинематические соединения
- •5) Структурный синтез механизмов
- •6) Единый принцип л.В.Ассура образования м-ов.
- •7) Замена высших пар 4-го класса в плоских м-мах кинематическими низшими парами 5-го класса.(Рисунки смотреть в конспекте).
- •8) Порядок структурного анализа механизмов.
- •9) Понятие термина «машина». Классификация машин
- •10) Задачи и методы кинематического анализа. Масштабные коэффициенты
- •11) Метод планов. Построение планов скоростей (пс) и определение скоростей.
- •12) Метод планов. Построение плана ускорений (пу)
- •13) Построение пс для механизмов, имеющих кулисные и поступательные пары. Определение величины и направлений угловых скоростей звеньев механизма
- •1 4) Построение пу для механизмов, имеющих кулисные и поступательные пары. Определение величины и направлений угловых ускорений звеньев механизма
- •1 5) Особенности плана скоростей и плана ускорений
- •16) Графическое дифференцирование. Определение масштабных коэффициентов
- •17) Задачи динамического анализа машин и механизмов.
- •18)Динамическая модель машинного агрегата.
- •19. Приведенные моменты инерции механизма.
- •20 Приведенные моменты сил сопротивления и сил движущих.
- •21. Определение приведенной силы.
- •22) Диаграмма работ от сил движущихся и сил полезного сопротивления. График изменения кинематической энергии рычажного механизма.
- •2 3) Определение момента инерции маховика методом Виттенбауэра
- •24) Механические передачи(редукторы,мультипликаторы,коробки скоростей,вариаторы,фрикционные передачи).
- •25) Виды зубчатых механизмов
- •26.Кинематический анализ зубчатых механизмов с неподвижными осями. Формулы для подсчета передаточного отношения.
- •27. Рядовые, ступенчатые, червячные передачи конические. Определение передаточных отношений и их передач.
- •28. Кинематический анализ зубчатых механизмов с подвижными осями колес (планетарные зубчатые передачи), 4-х звенный планетарный механизм Джемса. Формула Виллиса.
- •29. Планетарные редукторы со сдвоенными сателлитами. Редуктор Джемса. Редуктор Давида. Определение передаточных отношений.
- •30. Подбор чисел зубьев планетарного редуктора (соосность, соседство, условие сборки).
- •31) Эвольвента окружности и ее основные свойства.
- •33) Основные параметры зубчатых передач (эвольвентное зацепление), коэффициент относительного скольжения.
- •35) Способы изготовления зубчатых колёс
- •38*) Размеры корригированных зубчатых колес.
- •39) Межцентровое расстояние пары колес (нулевая передача, положительная передача, отрицательная передача).
- •40) Силовой расчёт. Его задачи. Классификация сил (внешние и внутренние)
- •41) Опред-е сил инерции и мом-ов инерции при вращ-ом,поступ-ом,и сложном движ-ях. Принцип Даламбера
- •42) Порядок силового расчёта(пример)
- •43) Теорема Жуковского о жестком рычаге
- •45) Кулачковые механизмы. Классификация кулачковых мех-ов.
- •46) Основные кинематические и геометрические параметры кулачковых механизмов. Условие выбора ролика.
- •47) Кинематических размеров км. Минимальный радиус вектора кулачка (км с коромысловый)
- •48) Минимальный радиус вектора кулачка (км и возвратно-поступательным толкателем, с толкателем)
- •51) Построение цпк и дпк для кулачковых механизмов с коромысловым толкателем.
- •52). Построение цпк и дпк для кулачковых механизмов с поступательным толкателем.
- •53)Построение цпк и дпк для кулачковых механизмов с .С тарельчатым толкателем.
- •54. Законы (режимы) движения кулачковых механизмов.И их влияние на работу механизмов.
- •55. Трение в механизмах и машинах. Виды и классификация трения.
- •56. Режимы движения механизмов
- •57) Определение кпд машин при последовательном, параллельном и смешанном соединении механизмов.
- •58) Основы определения теории машин-автоматов.
6) Единый принцип л.В.Ассура образования м-ов.
Возможны
следующие варианты сочетаний
|
2 |
4 |
6 |
|
3 |
6 |
9 |
класс |
2 |
3 |
4 |
Первичный м-зм состоит из стойки и одного подвижного звена и обладает степенью подвижности W=3*1-2*1=1; Число первичных м-мов равно числу степеней подвижности всего м-ма. Если от м-ма отделить первичный м-зм (начальное звено), то освободившаяся ведомая кинематическая цепь будет иметь степень подвижности равную нулю, если её присоединить к стойке освободившимися звеньями.
W=3*3-2*4=1 W=3*1-2*1=1 W=3*2-2*3=0
(Группа
) (Механизм) (Начальное звено)
 Кинематическая
цепь, имеющая степень подвижности равную
нулю получила название структурной
группы Ассура.
Кинематическая
цепь, имеющая степень подвижности равную
нулю получила название структурной
группы Ассура.
Если все кинематические пары 4 класса заменить парами 5 класса, то формула Чебышева примет вид:

Приравняем
к нулю левую часть формулы, т. к. у группы
Ассура W=
0 . Тогда
 и
т. д.
и
т. д.
В соответствии с числом кинематических пар, входящих в замкнутый контур звеньев проводится классификация групп.
В соответствии с числом не присоединенных
кинематических пар определяют порядок
группы. Класс и порядок м-мов определяется
наивысшим классом и порядком группы,
входящей в его состав.
соответствии с числом не присоединенных
кинематических пар определяют порядок
группы. Класс и порядок м-мов определяется
наивысшим классом и порядком группы,
входящей в его состав.
Разделять м-зм на группы нужно, начиная с наиболее удаленной от начального звена.
7) Замена высших пар 4-го класса в плоских м-мах кинематическими низшими парами 5-го класса.(Рисунки смотреть в конспекте).
 При
изучении структуры и кинематики плоских
м-мов во многих случаях удобно заменять
высшие пары кинематическими цепями или
звеньями, входящими только в низшие
вращательные и поступательные пары 5
класса. При этой замене должно
удовлетворяться условие, чтобы м-м,
полученный после такой замены, обладал
прежней степенью свободы и чтобы
сохранились относительные в рассматриваемом
положении дв-я всех его звеньев. Рассмотрим
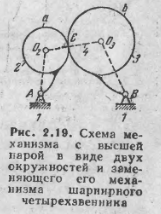
трехзвенный м-м, показанный на рис. 2.19.
М
При
изучении структуры и кинематики плоских
м-мов во многих случаях удобно заменять
высшие пары кинематическими цепями или
звеньями, входящими только в низшие
вращательные и поступательные пары 5
класса. При этой замене должно
удовлетворяться условие, чтобы м-м,
полученный после такой замены, обладал
прежней степенью свободы и чтобы
сохранились относительные в рассматриваемом
положении дв-я всех его звеньев. Рассмотрим
трехзвенный м-м, показанный на рис. 2.19.
М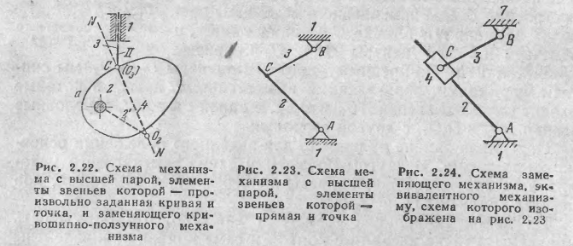 -м
состоит из двух подвижных звеньев 2
и 3,
входящих во
вращательные пары 5 класса А
и В
со стойкой
1 и
высшую пару С
4 класса,
элементы звеньев а и b
которой
представляют собою окружности радиусов
02С и
03С. Согласно
формуле (2.5) степень свободы механизма
будет = 1. W=3*n-2*P5-P4=3*2-2*2-1=1
Можно показать, что рассматриваемый
механизм может быть заменен эквивалентным
ему механизмом шарнирного четырехзвенника
А0203В. Высшая
нара 4 класса в точке С
заменяется
звеном 4,
входящим в
точках 02 и О3
во вращательные
пары 5 класса. Полученный в результате
замены механизм А0203B
называется
заменяющим
механизмом. Степень
свободы ‚W
заменяющего
механизма будет той же, что и у заданного
механизма. Имеем W=Зn—2р5=З*3—2*4=
1. Так как
элементы а и b
звеньев являются окружностями с центрами
в точках 02 и
О3, то
длина 0203
звена 4
оказывается постоянной. Точно так же
будут постоянными и длины АО2
и ВО2
звеньев 2
и З. Заменяющий
механизм А0203В
эквивалентен
заданному и с точки зрения законов
движения звеньев2 и З.
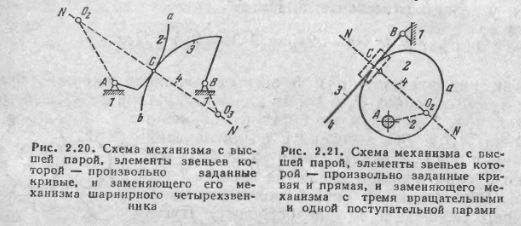
Рассмотренный
способ получения заменяющего м-а можно
обобщить. Пусть задан механизм с высшей
парой, элементы звеньев которой
представляют собой произвольно заданные
кривые а и b
(рис. 2.20). для
построения схемы заменяющего механизма
про водим
нормаль NN
в точке С
касания
кривых и отмечаем на ней центры 02 и О3
кривизны
кривых а и b.
По-прежнему
центры кривизны 02 и О3
мы считаем
шарнирами, образующими вращательные
пары, в которые входят условные звенья
АО2 и
0203, с
одной стороны, и условные звенья ВО3
и 0203, с другой
стороны. Описанная
замена правильна для заданного положения
основного м-а. В другом положении схема
заменяющего механизма останется той
же, размеры же его звеньев изменятся,
ибо центры кривизны 02 и О3
сместятся.
Из дифференциальной геометрии известно,
что окружность кривизны в точке касания
с кривой и сама кривая эквивалентны до
производных второго порядка включительно,
и поэтому заменяющий механизм эквивалентен
основному в такой же степени, т. е.
положения, скорости и ускорения
одноименных точек того и другого
механизма будут одинаковыми.Если один
из соприкасающихся элементов будет
представлять собой некоторую кривую,
а второй прямую b
(рис. 2.21), то центр крпвизны второго
профиля будет бесконечно удален. Условное
звено 4 в
этом случае будет входить в центре
кривизны 02
элемента 2
во вращательную
пару 5 класса. Вторая вращательная пара,
в которую должно входить звено 3,
имеет ось
вращения бесконечно удаленной и переходит
в поступательную пару также 5 класса.
далее возможен
случай, когда один из соприкасающихся
элементов -- кривая а, а другой — точка
С (рис.
2.22). В этом
случае центр кривизны О
элемента С
совпадает
с самой точкой С
и поэтому
условное звено 4
должно
ВХОДИТЬ в две вращательные пары 5
класса — во
вращательную пару с осью, проходящей
через центр кривизны 02 криволинейного
элемента а, и во вращательную пару с
осью, проходящей через точку С.
В том
случае, когда одним элементом является
прямая АС, а
другим — точка С
(рис. 2.23),
замена сводится
к постановке условного звена 4, входящего
в одну поступательную и одну вращательную
пары. Ось вращательной пары и ось движения
поступательной пары должны проходить
через точку соприкосновения С.
Заменяющий
м-м показан на рис. 2.24. Таким образом,
любой плоский механизм с высшими парами
4 класса может быть заменен механизмом,
в состав которого входят только низшие
кинематические пары 5 класса.Если все
высшие пары 4 класса в плоском механизме
заменены низшими парами, то структурная
формула (2.5) для заменяющего механизма
получит вид W=3n-2P5
-м
состоит из двух подвижных звеньев 2
и 3,
входящих во
вращательные пары 5 класса А
и В
со стойкой
1 и
высшую пару С
4 класса,
элементы звеньев а и b
которой
представляют собою окружности радиусов
02С и
03С. Согласно
формуле (2.5) степень свободы механизма
будет = 1. W=3*n-2*P5-P4=3*2-2*2-1=1
Можно показать, что рассматриваемый
механизм может быть заменен эквивалентным
ему механизмом шарнирного четырехзвенника
А0203В. Высшая
нара 4 класса в точке С
заменяется
звеном 4,
входящим в
точках 02 и О3
во вращательные
пары 5 класса. Полученный в результате
замены механизм А0203B
называется
заменяющим
механизмом. Степень
свободы ‚W
заменяющего
механизма будет той же, что и у заданного
механизма. Имеем W=Зn—2р5=З*3—2*4=
1. Так как
элементы а и b
звеньев являются окружностями с центрами
в точках 02 и
О3, то
длина 0203
звена 4
оказывается постоянной. Точно так же
будут постоянными и длины АО2
и ВО2
звеньев 2
и З. Заменяющий
механизм А0203В
эквивалентен
заданному и с точки зрения законов
движения звеньев2 и З.
Рассмотренный
способ получения заменяющего м-а можно
обобщить. Пусть задан механизм с высшей
парой, элементы звеньев которой
представляют собой произвольно заданные
кривые а и b
(рис. 2.20). для
построения схемы заменяющего механизма
про водим
нормаль NN
в точке С
касания
кривых и отмечаем на ней центры 02 и О3
кривизны
кривых а и b.
По-прежнему
центры кривизны 02 и О3
мы считаем
шарнирами, образующими вращательные
пары, в которые входят условные звенья
АО2 и
0203, с
одной стороны, и условные звенья ВО3
и 0203, с другой
стороны. Описанная
замена правильна для заданного положения
основного м-а. В другом положении схема
заменяющего механизма останется той
же, размеры же его звеньев изменятся,
ибо центры кривизны 02 и О3
сместятся.
Из дифференциальной геометрии известно,
что окружность кривизны в точке касания
с кривой и сама кривая эквивалентны до
производных второго порядка включительно,
и поэтому заменяющий механизм эквивалентен
основному в такой же степени, т. е.
положения, скорости и ускорения
одноименных точек того и другого
механизма будут одинаковыми.Если один
из соприкасающихся элементов будет
представлять собой некоторую кривую,
а второй прямую b
(рис. 2.21), то центр крпвизны второго
профиля будет бесконечно удален. Условное
звено 4 в
этом случае будет входить в центре
кривизны 02
элемента 2
во вращательную
пару 5 класса. Вторая вращательная пара,
в которую должно входить звено 3,
имеет ось
вращения бесконечно удаленной и переходит
в поступательную пару также 5 класса.
далее возможен
случай, когда один из соприкасающихся
элементов -- кривая а, а другой — точка
С (рис.
2.22). В этом
случае центр кривизны О
элемента С
совпадает
с самой точкой С
и поэтому
условное звено 4
должно
ВХОДИТЬ в две вращательные пары 5
класса — во
вращательную пару с осью, проходящей
через центр кривизны 02 криволинейного
элемента а, и во вращательную пару с
осью, проходящей через точку С.
В том
случае, когда одним элементом является
прямая АС, а
другим — точка С
(рис. 2.23),
замена сводится
к постановке условного звена 4, входящего
в одну поступательную и одну вращательную
пары. Ось вращательной пары и ось движения
поступательной пары должны проходить
через точку соприкосновения С.
Заменяющий
м-м показан на рис. 2.24. Таким образом,
любой плоский механизм с высшими парами
4 класса может быть заменен механизмом,
в состав которого входят только низшие
кинематические пары 5 класса.Если все
высшие пары 4 класса в плоском механизме
заменены низшими парами, то структурная
формула (2.5) для заменяющего механизма
получит вид W=3n-2P5

 и n
и n