3) Кинематические цепи. Кинематические соединения

Классификация кинематических пар. Кинематические пары (КП) классифицируются по следующим признакам:

1. По виду места контакта (места связи) поверхностей звеньев:

- низшие, в которых контакт звеньев осуществляется по плоскости или поверхности ( пары скольжения );

- высшие, в которых контакт звеньев осуществляется по линиям или точкам (пары, допускающие скольжение с перекатыванием).

2. по относительному движению звеньев, образующих пару:

- вращательные;

-поступательные;

- винтовые;

- плоские;

-сферические.

3. по способу замыкания (обеспечения контакта звеньев пары):

- силовое (за счет действия сил веса или силы упругости пружины); - геометрическое (за счет конструкции рабочих поверхностей пары).

4. по числу условий связи, накладываемых на относительное дв-е звеньев ( число условий связи определяет класс кин. пары );

5. по числу подвижностей в относительном движении звеньев.

Кинем. цепь – это система звеньев, связанных между собой кинем. парами.

Кинем. цепи могут быть: простыми (цепь, в которой каждое звено входит не более чем в 2 кин. пары) и сложными ( цепь, в которой хотя бы одно из звеньев образует более 2 кин.пар).

4) Механизмы плоские и пространственные. Число степеней свободы механизма и его определение.

Плоский м-зм - м-зм, в котором все точки и звенья перемещаются в плоскостях // между собой.

Пространственный м-зм – м-зм, в котором все точки и звенья перемещаются в плоскостях не параллельных между собой.

W число степеней свободы м-ма.

W=1 – для плоских м-мов,

W не = 1 – для пространственных м-мов Определение числа степеней свободы м-ма: W=3*n-2*P5-P4- формула Чебышева для плоских м-мов.

где W- число степеней свободы n-число подвижных звеньев

Р5-число пар 5-го класса м-ма

Р4-число пар 4-го класса м-ма

Для плоских м-мов если W не = 1, то допущена ошибка, либо присутствуют звенья, создающие лишнюю степень свободы.

5) Структурный синтез механизмов

О сновной принцип образования механизмов был впервые сформулирован русским ученым Ассуром. Им был продолжен и развит метод образования м-мов путем последовательного наслоения кинематических цепей, обладающих определенными структурными св-ми. Этот метод легко проследить, рассматривая какой либо конкретный м-зм, например м-зм, показанный на рис: 3.1. Этот м-зм имеет пять подвижных звеньев, образующих семь кинематических пар 5 класса. Следовательно, по формуле Чебышева (2.5) число его степеней свободы равно W=3*n-2*P5=3*5-2*7=1 т. е. м-зм, показанный на рис. 3.1, обладает одной степенью свободы. Выберем в качестве начального звено 2. Тогда м-зм будет состоять из начального звена 2, обладающего одной степенью свободы, стойки 1 и звеньев, образующих кинематическую цепь, состоящую из звеньев 3, 4, 5 и 6. Процесс образования этого м-ма можно представить как последовательное присоединение к начальному звену 2 и к стойке 1 кинематической цепи, состоящей из звеньев З и 4. Тогда получим четырехзвенный механизм АВCD, обладающий одной степенью свободы. Далее к звену 4 механизма AВСD и стойке 1 присоединим кинематическую цепь, состоящую из звена 5 и ползуна 6. Тогда получим шестизвенный м-зм, обладающий также одной степенью свободы. Нетрудно теперь установить определенную закономерность процесса образования м-ма. В самом деле, любой м-зм имеет одно неподвижное звено (стойку). У м-ма, показанного на рис. З.1, стойкой будет звено 1. Далее, м-зм должен иметь число начальных звеньев, равное числу его степеней свободы. В нашем случае м-зм (рис. 3.1) обладает одним начальным звеном 2, так как степень свободы ме-ма согласно (3.1) равна W=1Так как после присоединения звеньев 3, 4, 5 и б число степеней свободы всего м-ма осталось равным W=1, то,

следовательно, кинематическая цепь, состоящая из звеньев 3, 4, 5 и 6, присоединенных к начальному звену 2 и стойке 1, обладает нулевой степенью свободы относительно тех звеньев, к которым эта цепь присоединяется. При последовательном присоединении групп необходимо руководствоваться определенными правилами. При образовании м-ма с одной степенью свободы первая группа присоединяется свободными элементами звеньев к начальному звену и к стойке. Последующие группы могут присоединиться к любым звеньям полученного м-ма только так, чтобы звенья группы обладали подвижностью друг относительно друга. Пусть, например, мы имеем четырехзвенный механизм АВСD (рис. 3.2), образованный начальным звеном 2, стойкой 1 и группой, состоящей из звеньев 3 и 4. Следующая группа, состоящая из звеньев 5 и 6, может быть присоединена к любым двум разным звеньям механизма, например к звеньям 3 и 4 (рис. 3.2), но не к одному и тому же звену. Так, например, если присоединить звенья 5 и 6 к одному и тому же звену 3 (рис. 3.2). то контур FEG’, образованный звеньями 3, 5 и 6, будет жестким, т. е. будет фермой. Нетрудно видеть, что для того, чтобы после присоединения группы ее звенья имели подвижность относительно тех звеньев, к которым группа присоединена, необходимо, чтобы замкнутый контур, образованный звеньями группы и звеньями, к которым она п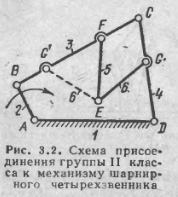 рисоединится, был подвижным контуром. Так, на рис. 3.2 контур GСFЕ будет обладать подвижностью. Нетрудно видеть, что для того, чтобы такой контур обладал подвижностью, необходимо, чтобы звенья контура входили бы не менее чем в четыре кинематические пары (пары F, Е,G и С на рис. 3.2).