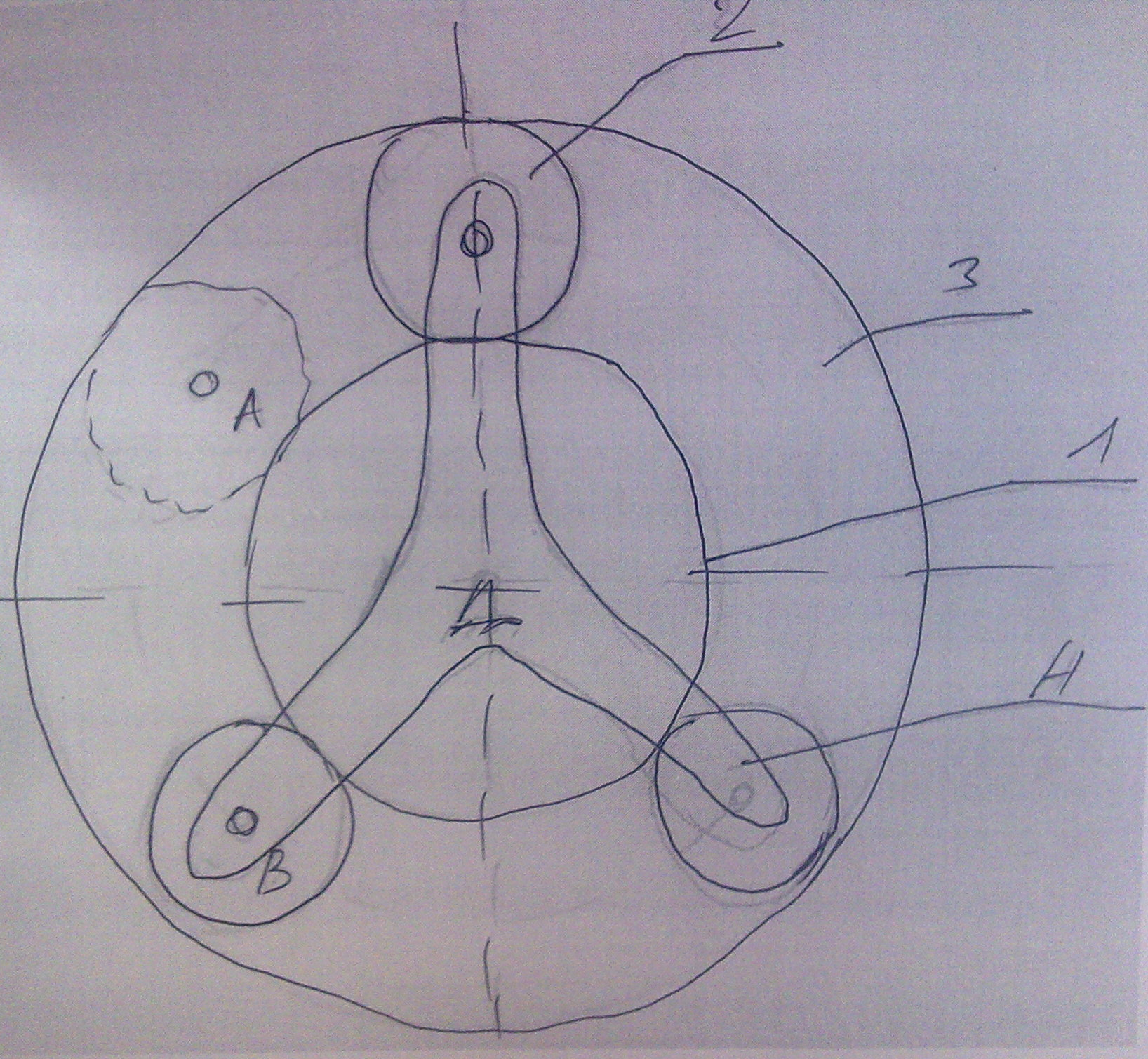
29. Планетарные редукторы со сдвоенными сателлитами. Редуктор Джемса. Редуктор Давида. Определение передаточных отношений.

- расчётная формула

, m=1

- расчётная формула.

Р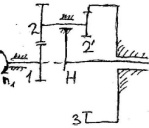 едуктор Джеймса- одно зацепление внешнее другое внутреннее. На одном валу неподвижно закреплено 2-а сателлита и этот вал несёт водило.

, т.к. m=1

- расчётная формула Джеймса.

Редуктор Давида- оба зацепления внешние

, т.к. m=2

- расчётная формула.

30. Подбор чисел зубьев планетарного редуктора (соосность, соседство, условие сборки).

Чтобы подобрать число зубьев рассмотрим 3 условия: соосности, соседства, сборки

Условие соосности - две передачи соосны если зубчатые колёса одной передачи имеют оси совпадают с осью другой передачи.

r₁+ r₂= r₃- r₂; =

m-модуль зацепления ,мм

Условие сборки: Проверяем редуктор на условие сборки =с где с- любое целое число. При сборке планетарного редуктора 1-вый пост сотелит полностью определяет взаимное расположение центральных колёс. Выполняется если с-целое число.

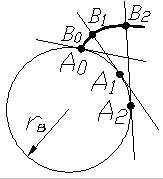
Условие соседства

выполняется когда расстояние между осями двух смежных сотелитов больше диаметра окружности их вершин. Z- число зубьев; к-число сотелитов(в маш строй к= 2—5) Окружности вершин сотелита не должны пересекаться – формула условия соседства. – возможное число сателлитов

31) Эвольвента окружности и ее основные свойства.

Наибольшее применение получили эвольвентные зубчатые передачи с профилем зубьев, очерченным по эвольвенте (рис. 72).

      Эвольвентой круга называется траектория точки, лежащей на прямой, которая перекатывается без скольжения по окружности радиуса r_в, называемой основной.          рис. 72  

  Эвольвента имеет следующие свойства:

 1) начинается с основной окружности;

 2) нормаль к эвольвенте является касательной к основной окружности;

 3) радиус кривизны эвольвенты в каждой её точке лежит на нормали к эвольвенте в этой точке.

Основная окружность представляет собой геометрическое место центров кривизны эвольвенты и является её эволютой.

3 2) Основными параметрами зубчатого колеса являются (рис. 75): 

        рис. 75        

z – число зубьев;

r_a – радиус (диаметр) окружности    выступов;

r_f – радиус (диаметр) окружности впадин;

r_b - радиус (диаметр) основной окружности;

r - радиус (диаметр) делительной окружности, т. е. окружности, которая  является  начальной  в станочном зацеплении колеса с режущим инструментом; р – шаг по делительной окружности;

h – высота зуба, равная h=h_a+h_f, где:

h_a – высота головки зуба;h_f – высота ножки зуба;

m – модуль зацепления, определяемый из условия:

,  т. е. 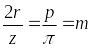  (измеряется в мм).

Величина m стандартизирована, а делительная окружность является окружностью стандартного модуля. Обычно размеры зубчатого колеса и зубьев выражаются через m.

Так, например: , где  - коэффициент  высоты головки зуба;

, где  - коэффициент  радиального зазора;

;  ;  , где α – угол исходного контура режущего инструмента.

Обычно для стандартных зубчатых колёс: ;  ;    α=20º.