27. Рядовые, ступенчатые, червячные передачи конические. Определение передаточных отношений и их передач.

Р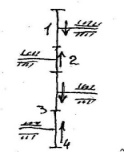 ядовые - характеризуются тем, что на каждом валу неподвижно закреплено по одному колесу, все валы параллельны. Передаточное отношение- i(u). m-число внешних зацеплений. 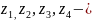число зубьев колёс.

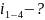
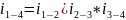
Через угловые скорости ω:

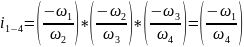
z-число зубчатых колёс

Д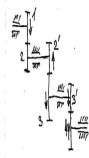 ля рядовых передач параметры промежуточных колёс на передаточное отношение не влияет, величину передаточных отношений формулируют входное и выходное звенья, промежуточный ряд колёс – паразитный ряд. Промежуточные колёса применяют для того чтобы сформировать соответственный знак передачи, либо необходимость вписаться при заданном предат. Отношении в заданное межосевое расстояние.

При числе колёс n: 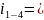- для рядовой передачи. m-число внешних зацеплений.

- обратная задача

Ступенчатые передичи-передачи в которых на входном и выходном валу неподвижно закреплено по одному колесу на промеж. Валах неподвижно закреплено по 2 колеса. Все валы между собой параллельны.

z-известны. Для каждой пары колёс модуль должен быть единым.

Через угловые скорости:

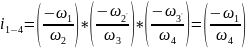
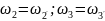
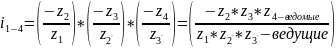
На одно промеж. Валу зубчатые колёса, могут иметь не равное число зубьев. n-число колёс

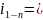-ступенчатая передача

Конические передачи-

1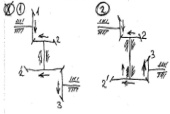 вид: на каждом валу неподвижно закреплено по одному колесу

Формулы применяются такие же что и для рядовой передачи но без учёта знака. Знак передачи определяется по методу стрелок.

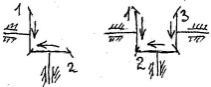–обратная задача

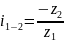
2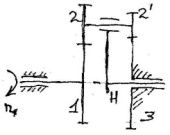 вид: на входном и выходном валу закреплено по 1 колесу , а на промеж. Валах по 2.

Для таких видов коническ. передач применяется ф-ла перед. отношения- для ступенчатых передач без учёта , знак передачи опред. по методу стрелок.

–обратная задача

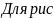.1 - 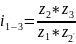Для рис.2-

Ч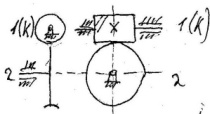 ервячные передачи – оси взаимноперпендикулярны и явл. Скрещивающимися и не имеют общей точки прикосновения.

1- червяк, 2- червячное колесо, k-число заходов червяка.

( ,

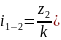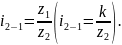
28. Кинематический анализ зубчатых механизмов с подвижными осями колес (планетарные зубчатые передачи), 4-х звенный планетарный механизм Джемса. Формула Виллиса.

Планетарные м-мы - это зубчат. передачи имещие подвижную ось. Обязательно наличие звена-«водила». Все оси на которые закреплены зубчатые колёса параллельны между собой.

Если W=1-планетарная зубчатая передача.

W≠1-дифференциальная

Редуктор Джемса. Это 4-х звенный планетарный механизм.

1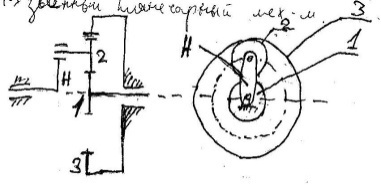 -центральное колесо(подвижное), может быть неподвижным, когда колесо 3 неподвижно(-солнечное центральное колесо), 2-саттелит-подвижное колесо(вращается вокруг колеса 1), 3-центральное неподвижное, может быть подв., когда колесо 1 неподвижно.(-опорное колесо),

Н-водило- подвижное звено несущее вал сателлита. (1-2)-вр.п., 5 кл.;(2-Н)- вр.п., 5 кл.;

(Н-0)- вр.п., 5 кл.;(1-2),(2-3)-4 кл.

m=4-все звенья

n=3-подвижные звенья(1,2,Н)

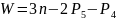
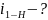-для определения применяем метод обращонного дв-я.

Всей системе придают такую угловую скорость которая = угловой скорости водила Н, но противиположна по направлению. .

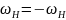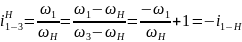
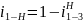-исходная формула Виллеса