Выполнение арифметических операций в двоичной системе счисления.
Во всех позиционных системах счисления арифметические операции выполняются по одним и тем же правилам:
1) справедливы одни и те же законы арифметики: коммутативный, ассоциативный, дистрибутивный;
2) справедливы правила сложения, вычитания и умножения столбиком;
3) правила выполнения арифметических операций опираются на таблицы сложения и умножения.
Сложение.
При сложении столбиком двух цифр справа налево в двоичной системе счисления, как в любой позиционной системе, в следующий разряд может переходить только единица.
Результат сложения двух положительных чисел имеет либо столько же цифр, сколько у максимального из двух слагаемых, либо на одну цифру больше, но этой цифрой может быть только единица.
Вычитание.
При выполнении операции вычитания всегда из большего по абсолютной величине числа вычитается меньшее и у результата ставится соответствующий знак.
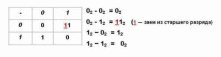
Умножение. Операция умножения выполняется с использованием таблицы умножения по обычной схеме (применяемой в десятичной системе счисления) с последовательным умножением множимого на очередную цифру множителя.
Деление Операция деления выполняется по алгоритму, аналогичному алгоритму выполнения операции деления в десятичной системе счисления.
Логика. Понятие, высказывание, умозаключение. Логические высказывания. Истинность высказывания.
Логика - это наука о формах и способах мышления.
Законы логики отражают в сознании человека свойства, связи и отношения объектов окружающего мира. Логика позволяет строить формальные модели окружающего мира, отвлекаясь от содержательной стороны. Мышление всегда осуществляется в каких-то формах. Основными формами мышления являются понятие, высказывание и умозаключение. Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта.
Понятие имеет две стороны: содержание и объем.
Содержание понятия составляет совокупность существенных признаков объекта. Чтобы раскрыть содержание понятия, следует найти признаки, необходимые и достаточные для выделения данного объекта из множества других объектов.
Объем понятия определяется совокупностью предметов, на которую оно распространяется. Объем понятия «персональный компьютер» выражает всю совокупность (сотни миллионов) существующих в настоящее время в мире персональных компьютеров.
Умозаключение – это форма мышления, с помощью которой из одного или нескольких суждений (посылок) может быть получено новое суждение (заключение).
Как и любая другая форма мышления, умозаключение, так или иначе, воплощается в языке. Если понятие выражается отдельным словом (или словосочетанием), а высказывание – отдельным предложением (или сочетанием предложений), то умозаключение всегда есть связь нескольких (двух или более) предложений, хотя не всякая связь двух или более предложений – непременно умозаключение. В русском языке эта связь выражается словами “следовательно”, “значит”, “таким образом” и другими, либо словами “потому что”, “так как”, и т.п.
Высказывание – это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними.Высказывание может быть либо истинно, либо ложно.
По форме высказывание является повествовательным предложением.
Высказывание не может быть выражено повелительным или вопросительным предложением, так как оценка их истинности или ложности невозможна. Всякое высказывание или истинно, или ложно; быть одновременно и тем и другим оно не может.
Простые высказывания в алгебре логики обозначаются заглавными латинскими буквами:
А = {Аристотель - основоположник логики}.
В = {На яблонях растут бананы}.
Истинному высказыванию ставится в соответствие 1, ложному — 0. Таким образом, А= 1, В = 0.
Алгебра логики отвлекается от смысловой содержательности высказываний. Ее интересует только один факт — истинно или ложно данное высказывание, что дает возможность определять истинность или ложность составных высказываний алгебраическими методами.