3. Решение транспортной задачи методом Фогеля, определение общего пробега, пробега с грузом и транспортной работы для маятниковых маршрутов.

Метод Фогеля позволяет без использования ЭВМ получить оптимальный или близкий к нему результат. Решение проводится по следующему алгоритму:

- исходная матрица дополняется столбцом и строкой. Затем в каждой строке и каждом столбце матрицы находятся два наименьших элемента, и определяется абсолютная разность между ними, которая заносится соответственно разности по строке в столбец разностей, разности по столбцам – в строку разностей. Если две клетки в одной и той же строке или столбце имеют одинаковые значения, то разность для этой строки или столбца принимается равной нулю.

- выбирается наибольшая величина разности независимо от того, стоит ли она в столбце или строке разностей. В клетку с минимальным элементом в данной строке или столбце заносится максимально возможная загрузка, учитывая при этом соотношение ресурсов поставщика и спрос потребителя. Если окажется, что спрос потребителя полностью удовлетворен или ресурс поставщика полностью исчерпан, то данная строка или столбец матрицы из дальнейшего рассмотрения исключается.

- после заполнения и последующего исключения клетки матрицы разности пересчитываются, и операция повторяется вновь до тех пор, пока не будет составлен допустимый план закрепления потребителей за поставщиками.

Пробег с грузом (L_г), общий пробег (L_о) и транспортная работа (Р) для маятниковых маршрутов определяются по формулам:

(2)

(3)

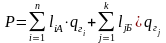(4)

где n, k – количество пунктов, закрепленных за грузоотправителями А и Б соответственно;

l_iA, l_jБ – расстояние от соответствующего грузоотправителя до i-ого и j-ого грузополучателя, км;

- масса груза, перевозимая i-ому и j-ому грузополучателю соответственно, т.

В таблице 3 приведены расстояния между пунктами погрузки и пунктами разгрузки, полученные в процессе выполнения задания 2 курсовой работы.

Для исходных данных, приведенных в Приложении 1, требуется определить план доставки груза. По формуле (1) были определены расстояния между пунктами, результат приведен в табл. 1

Таблица 3

Расстояния между пунктами транспортной сети

Пункт погрузки	Расстояние до пункта разгрузки, км
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3	6	7	6	5	14	4
Б	11	11	7	4	13	0	3	12	7	11

Дополним таблицу кратчайших расстояний строкой и столбцом разностей.

В первой строке два наименьших элемента - 3 и 4, поэтому разность составит 1, во второй строке два наименьших элемента 3 и 0 (табл.3). Наибольшая величина разности, равная 7, находится в 5,6, 8, 9 и 10-м столбце. Выбираем 2-го грузоотправителя.

Таблица 4

Исходная матрица для метода Фогеля

Пункт погрузки	Расстояние до пункта разгрузки, км										Столбец разности
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3	6	7	6	5	14	4	1
Б	11	11	7	4	13	0	3	12	7	11	3
Строка разностей	6	1	3	1	7	7	3	7	7	7

Таблица 5

Матрица для метода Фогеля после исключения 6-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км											Столбец разности
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3	6		6	5	14	4	1
Б	11	11	7	4	13		3	12	7	11	1
Строка разностей	6	1	3	1	7		3	7	7	7

Таблица 6

Матрица для метода Фогеля после исключения 8-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км										Столбец разности
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3	6		6		14	4		1
Б	11	11	7	4	13		3		7	11		1
Строка разностей	6	1	3	1	7		3		7	7

Таблица 7

Матрица для метода Фогеля после исключения 9-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км										Столбец разности
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3	6		6			4		1
Б	11	11	7	4	13		3			11		1
Строка разностей	6	1	3	1	7		3			7

Таблица 8

Матрица для метода Фогеля после исключения 10-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км											Столбец разности
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3	6		6				1
Б	11	11	7	4	13		3				1
Строка разностей	6	1	3	1	7		3

Таблица 9

Матрица для метода Фогеля после исключения 5-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км										Столбец разности
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3			6					1
Б	11	11	7	4			3					1
Строка разностей	6	1	3	1			3

Таблица 10

Матрица для метода Фогеля после исключения 1-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км											Столбец разности
	1	2	3	4	5	6	7	8	9	10
А		10	4	3			6				1
Б		11	7	4			3				1
Строка разностей		1	3	1			3

Таблица 11

Матрица для метода Фогеля после исключения 3-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км										Столбец разности
	1	2	3	4	5	6	7	8	9	10
А		10		3			6					3
Б		11		4			3					1
Строка разностей		1		1			3

Таблица 12

Матрица для метода Фогеля после исключения 7-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км										Столбец разности
	1	2	3	4	5	6	7	8	9	10
А		10		3							7
Б		11		4							7
Строка разностей		1		1

Таблица 13

Матрица для метода Фогеля после исключения 4-го столбца

Пункт погрузки	Расстояние до пункта разгрузки, км										Столбец разности
	1	2	3	4	5	6	7	8	9	10
А		10
Б		11
Строка разностей		1

Закрепление грузоотправителей за грузополучателями отражено в таблице 14. В столбце «Итого» приведено количество груза, которое должно быть у грузоотправителя, найденное как сумма потребностей закрепленных за ним грузополучателей.

Таблица 14

Оптимальное закрепление пунктов разгрузки за поставщиками

Пункт погрузки	Расстояние до пункта разгрузки, км											Итого
	1	2	3	4	5	6	7	8	9	10
А	5	10	4	3	6			5		4	22,17
Б						0	3		7		6,61
Объем груза, т.	3,69	4,30	3,10	3,49	1,67	0,07	1,20	1,42	5,34	4,50	28,78

Найдем пробег с грузом, общий пробег и транспортную работу для маятниковых маршрутов.

Пробег с грузом (Lг) находится по формуле:

,

где n, k – количество пунктов, закрепленных за грузоотправителями А и Б соответственно;

l_iA, l_jБ – расстояние от соответствующего грузоотправителя до i-ого и j-ого грузополучателя, км.

L _г: (5+10+4+3+6+5+4)+(0+3+7)= 95 км

Общий пробег (Lо) находится по формуле:

L_о: 2*47 = 94 км

Транспортная работа (P) находится по формуле:

, где - масса груза, перевозимая i-ому и j-ому грузополучателю соответственно, т.

P=(5*3,69+10*4,3+4*3,1+3*3,49+6*1,67+0*0,07+3*1,2+5*1,42+7*5,34+4*4,5)=160,42 ткм