4. Физический смысл производной. Мгновенная скорость изменения функции, ускорение и градиент

Физический смысл производной состоит в том, что она определяет быстрота (темп) изменения функции.

Рассмотрим пример прямолинейного движения. Скорость тела равна отношению пути ΔS, пройденного телом за время Δt, к этому промежутку времени v = . Если движение неравномерное, то отношение является средней скоростью на этом участке пути, а скорость, соответствующая каждому данному моменту времени, называется мгновенной скоростью движения и определяется как предел отношения при Δ t→0, т.е.

Обобщая полученный результат, можно утверждать, что производная функции f(x) по времени t является мгновенной скоростью изменения функции. Понятие мгновенной скорости относится не только к механическим движениям, но и к любым процессам, развивающимся во времени. Можно найти скорость сокращения или расслабления мышцы, скорость кристаллизации раствора, скорость отвердевания пломбировочного материала, скорость распространения эпидемического заболевания и др.

Значение мгновенного ускорения во всех этих процессах равно производной функции скорости по времени:

. (5)

В механике — вторая производная пути по времени.

Понятие производной, как величины, характеризующей быстроту изменения функции, применяется для разных зависимостей. Например, надо узнать, как быстро изменяется температура вдоль металлического стержня, если нагревать один из его концов. В данном случае температура - функция координаты x, т.е. T = f(x) и характеризует темп изменения температуры в пространстве.

Производную некоторой функции f(x) по координате x называют градиентом этой функции (часто используется сокращение grad от лат. gradient). Градиенты различных переменных – это векторные величины, всегда направленные в сторону увеличения значения переменных.

Отметим, что градиенты многих величин являются одной из первопричин обменных процессов, происходящих в биологических системах. Это, например, градиент концентрации , градиент электрохимического потенциала (μ – греческая буква «мю»), градиент электрического потенциала .

При малых Δx можно записать:

. (6)

5. Графики производных функций

В практической медицине часто приходится сопоставлять график изменения некоторой величины, например, со временем с графиком производной этой величины. В частности, в методе, называемом реопародонтография регистрируется зависимость объема кровенаполнения V исследуемого участка сосудистой системы от времени, т.е. V(t), и зависимость первой производной этой функции, которая определяет изменение скорости кровенаполнения. Примеры можно продолжить.

Д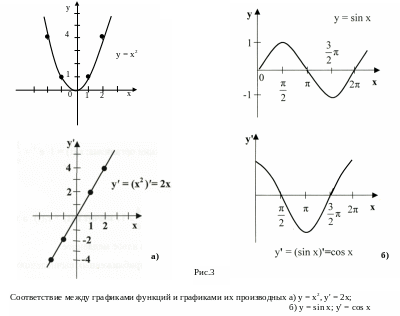 ля нескольких простых функций приведем графики самих функций и их производных.

6. Дифференциал функции и его применение в приближенных вычислениях

Дифференциал заданной функции y = f(x) равен произведению значения производной этой функции в данной точке x₀ на дифференциал аргумента (d – символ дифференциала):

(7)

Дифференциал независимой переменной равен приращению этой переменной: dx = Δx.

Дифференциал функции равен ее приращению только при достаточно малых приращениях Δх:

Δy ≈ dy (8)

Из формулы (7) с учетом соотношения (8) получаем:

, (9)

Формула (9) может использоваться для нахождения приближенного приращения функции и оценки значения градиента функции в соответствии с соотношением (6).

Приведем несколько примеров.

1. Найдем приближенное приращение функции y = 2x² + 7 при x₀ = 2 и

Δx = 0,0001.

Решение: ; y' = 4x или Δy ≈ 4x Δx

Таким образом, Δу ≈ 4 · 2 · 0,0001 = 0,0008.

2. Рассмотрим шарообразную клетку радиуса R (например, эритроцит в венозном русле), которая увеличивается в объеме, не изменяя формы. Объем (V = f(R)). Оценим изменение объема клетки ΔV, если ее радиус увеличился от 2,5 · 10^-3 до 2,6· 10^-3 см.

Решение: ΔV≈ dV = V'dR = = 4π R²ΔR = 7,85 · 10^-9 см³.