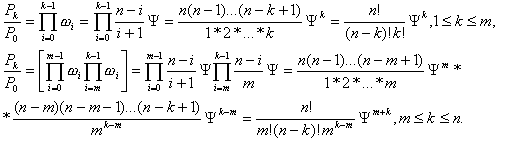- •Аналитические и имитационные модели
- •2. Композиция дискретных сиcтем.
- •Построение имитационой моделей системы.
- •4 Вопрос. Содержательное описание сложной системы. Выбор показателей качества моделируемой системы.
- •5 Вопрос. Содержательное описание сложной системы. Определение управляющих переменных системы
- •6 Вопрос. Содержательное описание сложной системы. Детализация описания режимов функционирования системы
- •7 Вопрос. Содержательное описание сложной системы. Составление описания внешней среды.
- •8. Системность – общее свойство материи. Признаки системности: структурированность системы, взаимосвязанность составляющих частей, подчиненность организации всей системы определенной цели.
- •Развитие системных представлений. Становление системного анализа.
- •Формулировка определения системного анализа.
- •Этапы системного анализа.
- •12. Изучение структуры системы, анализ ее компонентов, выявление взаимосвязей между компонентами системы.
- •13. Сбор данных о функционировании системы. Исследование информационных потоков.
- •14 Наблюдения и эксперименты над анализируемой системой.
- •15 Построение моделей. Проверка адекватности модели, анализ ее неопределенности и чувствительности, непротиворечивость, реалистичность, работоспособность модели.
- •16 Исследование ресурсных возможностей.
- •17 Формулирование проблемы.
- •18 Определение целей системного анализа.
- •19 Формирование критериев.
- •20 Генерирование альтернатив. Методы коллективной генерации идей. Разработка сценариев. Морфологические методы. Деловые игры. Методы экспертного анализа. Метод «Дельфи». Методы типа дерева целей.
- •21 Реализация выбора и принятия решений.
- •22 Внедрение результатов анализа.
- •23. Линейное программирование. Задача линейного программирования.
- •24. Линейное программирование. Пример Задачи линейного программирования.
- •25. Линейное программирование. Каноническая форма.
- •26. Линейное программирование. Метод полного исключения.
- •27. Линейное программирование. Пример применения метода полного исключения.
- •28. Линейное программирование. Симплексные преобразования.
- •29. Линейное программирование. Решение злп методом симплекс-таблиц.
- •30 .Двойственная задача линейного программирования. Структура и свойства двойственной задачи.
- •31 .Двойственная задача линейного программирования. Соотношение прямой и двойственной задачи.
- •32. Двойственная задача линейного программирования. Нахождение допустимых базисных решений. Метод искусственных переменных.
- •33. Нелинейное программирование. Оптимизация нелинейных функционалов. Ограничения в виде равенств.
- •34. Нелинейное программирование. Оптимизация нелинейных функционалов. Ограничения в виде неравенств.
- •35. Задачи и особенности теории массового обслуживания.
- •36. Обслуживающие системы и их классификация (структура и классификация смо, системы с неограниченным временем ожидания, системы с отказами, системы смешанного типа).
- •37. Входящий поток требований (определение простейшего потока, распределение вероятностей простейшего потока).
- •38. Распределение интервалов между двумя событиями (распределение Эрланга, время обслуживания).
- •39. Показатели эффективности обслуживающих систем
- •40 Системы массового обслуживания с ожиданием. Разомкнутая система с одним каналом обслуживания.
- •41 Системы массового обслуживания с ожиданием. Установившийся режим.
- •42 Системы массового обслуживания с ожиданием. Разомкнутая система с несколькими одинаковыми каналами обслуживания.
- •43 Системы массового обслуживания с ожиданием. Замкнутая система с ожиданием.
- •44 Системы массового обслуживания с ожиданием. Процесс размножения и гибели.
- •Аналитические и имитационные модели.
43 Системы массового обслуживания с ожиданием. Замкнутая система с ожиданием.
Система массового обслуживания с ожиданием - это такая система, которая имеет возможность ставить заявки в очередь, где эти заявки ожидают обслуживания. Разомкнутая система массового обслуживания – это система с неограниченным источником потока требований..Замкнутая система массового обслуживания – система, в которой поток требований ограничен. Замкнутые системы с ожиданием. При рассмотрении разомкнутых систем предполагалось, что источник обладает неограниченным числом требований. В настоящем параграфе рассмотрим случай, когда система предназначена для обслуживания конечного, постоянного числа требований. Будем предполагать, что как только требование обслужилось оно возвращается в источник. Схема такой системы изображена на рисунке 7.

Основное отличие разомкнутой системы от замкнутой состоит в том, что в разомкнутой системе интенсивность поступления требований - характеристика источника требований. В замкнутой системе потенциальное число требований является величиной постоянной. После обслуживания требования оно возвращается в источник. В замкнутой системе интенсивность поступления требований – характеристика конкретного объекта, поступающего в систему. Рассмотрим пример замкнутой системы. В организации имеется парк вычислительной техники в размере n штук и группа, обслуживающая вычислительную технику. В случае отказа компьютера он поступает в ремонт в указанную группу. Пусть – интенсивность отказа одной единицы техники (характеристика объекта). Данная величина характеризует интенсивность поступления на обслуживание данного объекта (только его одного). Потенциальное число заявок на обслуживание постоянное и равно n. Интенсивность входного потока требований зависит от числа исправно работающих объектов в источнике. В случае, когда все единицы вычислительной техники исправны, интенсивность потока требований равна n , после того как один компьютер откажет она станет (n - 1) и т.д. За время (t, t+dt) объект может потребовать обслуживания с вероятностью dt. За время (t, t+dt) объект, находящийся на обслуживании, может быть обслужен с вероятностью µdt. Если в некоторый момент времени число объектов, ожидающих обслуживания и обслуживаемых, равно k, то число объектов в источнике равно n - k. Вероятность поступления заявки на обслуживание хотя бы одного из данных объектов в интервале времени длительностью dt равна (n - k) dt. Таким образом, интенсивность потока требований изменяется скачкообразно всякий раз, когда компьютер выходит из строя, и возникает необходимость в его обслуживании.
44 Системы массового обслуживания с ожиданием. Процесс размножения и гибели.
Система массового обслуживания с ожиданием - это такая система, которая имеет возможность ставить заявки в очередь, где эти заявки ожидают обслуживания. Разомкнутая система массового обслуживания – это система с неограниченным источником потока требований. Замкнутая система массового обслуживания – система, в которой поток требований ограничен.
Процесс
размножения и гибели. Рассмотрим
систему обслуживания, в которой возможны
изменения состояний:![]() .
.
Если
в момент времени t система находится
в состоянии Ek, то
вероятность перехода Ek![]() Ek+1
в интервале длительностью dt равна
kdt.
Вероятность перехода Ek
Ek-1
в интервале длительностью dt равна
µkdt. Вероятность
перехода Er
Er+k(-k),
k
2
в интервале длительностью dt –
бесконечно малая величина по сравнению
с dt.
k
и µk зависят
только от k, где k – число
требований в системе. Граф переходов
для рассматриваемого случая представлен
на рисунке
8.
Ek+1
в интервале длительностью dt равна
kdt.
Вероятность перехода Ek
Ek-1
в интервале длительностью dt равна
µkdt. Вероятность
перехода Er
Er+k(-k),
k
2
в интервале длительностью dt –
бесконечно малая величина по сравнению
с dt.
k
и µk зависят
только от k, где k – число
требований в системе. Граф переходов
для рассматриваемого случая представлен
на рисунке
8.
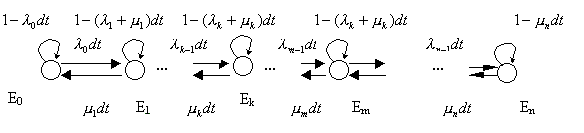
Рисунок 8 - Граф переходов замкнутой системы (процесс размножения и гибели)
Число состояний графа конечно и определяется числом элементов в источнике. Для данного графа можно записать дифференциальные уравнения состояний, которые называются уравнениями размножения и гибели:
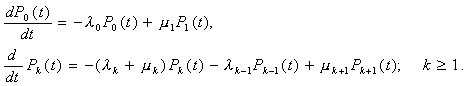
Используя эти уравнения, можно перейти к частным случаям исследования систем, если определить все k и µk.
45 Системы массового обслуживания с ожиданием. Замкнутые системы при m>n.
Замкнутые системы при n > m. Пусть – n потенциальное число требований, участвующих в процессе массового обслуживания, m – число каналов, µ – интенсивность обслуживания требования одним каналом. Будем считать, что все каналы идентичны. Интенсивность входящего потока зависит от числа поступивших требований. Если k - число поступивших требований, то k = (n - k) .
Интенсивность
обслуживания системы также зависит от
числа требований и вычисляется как

Граф переходов, соответствующий этому случаю, идентичен изображенному на рис. 3.7; при этом интенсивности переходов будут иметь значения
![]()
Дифференциальные уравнения для данного графа состояний:

Для установившегося режима получим стационарное решение:

Используя обозначения ТМО
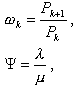
после элементарных преобразований получим:
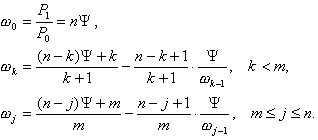
Последовательно решаем данную систему для k=1,2,…,m,…,n; получим результат

Теперь можно выразить вероятности Pk через P0 :
|
(52) |
Принимая во внимание, что сумма всех вероятностей равна единице, можно записать
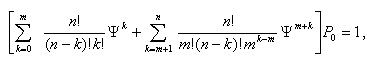
откуда имеем

Далее можно определить числовые характеристики системы. 1. Вероятность того, что в системе находится k требований, определяется из выражения (52). 2. Среднее число требований, ожидающих обслуживания,
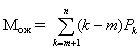 .
3.
Среднее число требований, находящихся
в системе обслуживания,
.
3.
Среднее число требований, находящихся
в системе обслуживания,
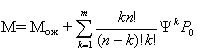 .
4.
Среднее число свободных каналов в
установившемся режиме
.
4.
Среднее число свободных каналов в
установившемся режиме
![]() .
5.
Коэффициент простоя требований, ожидающих
обслуживания,
.
5.
Коэффициент простоя требований, ожидающих
обслуживания,
 .
.
6. Коэффициент простоя каналов обслуживания

Содержание