27. Линейное программирование. Пример применения метода полного исключения.

Рассмотрим пример применения метода полного исключения Гаусса для исследования системы уравнений

x₁ + 2x₂ + x₃ + x₄ = 3

2x₁+ x₂ + x₃ + 3x₄ = 3

4x₁ + 5x₂ + 3x₃ + 5x₄ = 9

Расширенная матрица имеет вид

       

Первый шаг. В качестве первого направляющего элемента возьмем a₁₁=1. Умножив первую строку матрицы A на 2 , вычтем результат из второго уравнения и, умножив на 4 , вычтем результат из третьего уравнения; получим

   

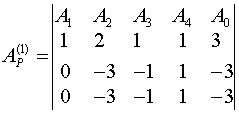
Второй шаг. Поскольку главная часть матрицы A_p⁽¹⁾ содержит отличные от нуля элементы , продолжим процесс исключения. Выберем элемент a₂₂⁽¹⁾= -3 в качестве направляющего элемента на втором шаге преобразования. Разделим вторую строку на -3, получим

   

Далее умножим вторую строку на 2 и вычтем результат из первой строки, умножим вторую строку на -3, результат вычтем из третьей строки, в итоге

Как видим, главная часть матрицы A_p⁽²⁾, состоящая из элементов a₃₃⁽²⁾ и a₃₄⁽²⁾, содержит только нули. Следовательно, процесс исключения заканчивается. Исследуем матрицу A⁽²⁾. Поскольку третья строка содержит только нулевые элементы, то это свидетельствует о том, что начальные уравнения были зависимыми, и, следовательно, она может быть отброшена. Тогда эквивалентная матрица системы уравнений будет выглядеть следующим образом:

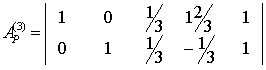
Теперь можно записать базисное решение

x₁=1,x₂=1,x₃=0,x₄=0, а также соответствующее общее решение

где - произвольные скаляры.

28. Линейное программирование. Симплексные преобразования.

Задачи линейного программирования, решаемые с помощью симплекс-метода, основываются на представлении решения в табличной форме. Рассмотрим последовательность действий при решении задачи линейного программирования

Пусть имеются линейная форма

c₁x₁+c₂x₂+...+c_nx_n---> max

и ограничения

Приведем матрицу ограничений к каноническому виду:

На следующем шаге составим таблицу.

c

c1

c2

c3

...

cj

...

cn

0

...

0

Bx

aio

A1

A2

A3

Aj

An

An+1

An+m

cn+1

xn+1

a1o

a11

a12

a13

a1j

a1n

1

0

cn+2

xn+2

a2o

a21

a22

a23

a2j

a2n

0

0

cn+i

xn+i

aio

ai1

ai2

ai3

aij

ain

0

0

cn+m

xn+m

amo

am1

am2

am3

amj

amn

0

1

aoo

a01

a02

a03

a0j

a0n

a0,n+1

a0,n+m

Нижняя строка элементов a_0k, , называется индексной. Элементы индексной строки вычисляется следующим образом: ; i = 1...n означает номер соответствующей строки. Поскольку на первом шаге заполнения таблицы все элементы c_n+i равны нулю, то элементам индексной строки присваиваются значения соответствующих элементов целевой функции данного столбца, взятые с обратным знаком, т.е. a_0k = -c_k. Последняя строка таблицы служит для определения направляющего столбца.

Элемент a₀₀ равен значению целевой функции, которое вычисляется по формуле , k - номер базисной переменной (индексация идет по строкам таблицы).

В столбце Bx записываются базисные переменные, на первом шаге в качестве базисных выбирают фиктивные переменные {x_n+k}, k = 1,m. В дальнейшем фиктивные переменные необходимо вывести из базиса.

В столбец C записываются коэффициенты при x_n+k, на первом шаге значения этих коэффициентов равны нулю.

Для перехода от базиса фиктивных переменных к базису реальных переменных применяют следующие правила:

- в качестве направляющего столбца выбирают столбец A_j, для которого выполняется условие.

, , при , т.е. выбирается минимальный элемент, при условии, что этот элемент отрицательный;

- выбирают направляющую строку, для чего каждый элемент столбца свободных членов делится на соответствующий элемент направляющего столбца. Из всех возможных соотношений выбирается минимальное a_i0/a_ij=min {a_r0/a_rj}

Далее выполняется шаг симплексных преобразований.

Переменная, которая соответствует направляющему столбцу, вводится в базис, а переменная, соответствующая направляющей строке, выводится из базиса. При этом для переменной, вводимой в базис, изменяется соответствующее значение коэффициента целевой функции. Вместо коэффициента c_n+i , соответствующего старой базисной переменной, в таблице записывается значение коэффициента целевой функции при переменной, вводимой в базис.

Если направляющий элемент a_ij, то переход от данной таблицы к следующей осуществляется с использованием следующих правил.

1. Для всех элементов направляющей строки ,

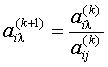
где k - номер шага (k =1,2,…),i - номер направляющей строки, j - номер направляющего столбца, , т.е. все элементы направляющей строки делим на направляющий элемент, в итоге направляющий элемент стал равным единице; a_il^(k+1)=1.

2. В направляющем столбце необходимо получить , a_rj^(k+1)=0 для всех , , при a_ij^(k+1)=1, т.е. в направляющем столбце должны быть все нули кроме направляющего элемента, который равен единице.

Для всех остальных элементов, включая индексную строку, производятся вычисления

, .

Симплексные преобразования повторяют до тех пор, пока

а) все a_0l 0 - это условие оптимальности базиса последней таблицы;

б) найдется такой элемент a_0j<0, при котором все элементы столбца a_rj 0, - это признак неограниченности целевой функции на множестве допустимых решений.