25. Линейное программирование. Каноническая форма.

Любую задачу линейного программирования можно свести к некоторой стандартной форме с ограничениями, записанными в виде уравнений. Это достигается путем введения свободных переменных во все ограничения. Свободная переменная учитывает разницу между правой и левой частями неравенства.

Пусть x_n+1- дополнительная переменная, которая численно равна

x_n+2- дополнительная переменная, которая численно равна

x_n+m- дополнительная переменная, которая численно равна

В результате получаем новую систему ограничений:

Целевая функция будет иметь вид

max F(x₁,x₂,...,x_n)=max(c₁x₁+c₂x₂+...+c_nx_n+0*x_n+1+0*x_n+2+...+0*x_n+m)

Или в матричной форме:

maxF(x)=max(c'x)

(5)

при условии AX₁+BX₂=P0, X₁>=0, X₂>=0,

где X₁ - вектор первоначальных переменных , X₂ - вектор свободных переменных;

B - единичная матрица m x m.

Отметим некоторые свойства, касающиеся системы ограничений:

1) уравнения линейно независимы, если ни одно из них не может быть получено из остальных путем алгебраических преобразований, т.е. никакие из них не являются следствием остальных;

2) если число независимых уравнений больше числа переменных, то такая система не имеет решения и называется несовместимой;

3) если число независимых уравнений равно числу переменных, то такая система имеет единственное решение, которое либо оптимально, если все компоненты положительны, либо недопустимо, если хотя бы одна из компонент отрицательна;

4) если удается найти множество неотрицательных значений , которое является решением системы m линейных уравнений с n+m неизвестными, то такое решение называют базисным, а ненулевые переменные - базисными переменными.

26. Линейное программирование. Метод полного исключения.

Пусть имеется система ограничений в виде

Перепишем данную систему уравнений в матричной форме: AX=A₀, и A_p=[A,A₀], где A_p- расширенная матрица.

Одну из строк расширенной матрицы умножают на число, отличное от нуля.

Из каждой строки расширенной матрицы (A_p) вычитают данную строку (из п.1) . Каждое такое преобразование называется преобразованием Гаусса. В результате получаем новую систему линейных уравнений, эквивалентную исходной.

Рассмотрим более подробно метод полного исключения.

1. Среди элементов матрицы A выбирают произвольный элемент, отличный от нуля. Этот элемент называют направляющим элементом шага. Строку и столбец, содержащие направляющий элемент, называют направляющей строкой и направляющим столбцом данного преобразования.

2. Все элементы направляющей строки расширенной матрицы (A_p) делят на направляющий элемент. В результате получают направляющую строку с направляющим элементом, равным единице. Далее из каждой строки матрицы вычитают новую направляющую строку, умноженную на элемент, который расположен на пересечении строки и направляющего столбца. Итак, пусть исходная система уравнений имеет вид

Возьмем в качестве направляющей строки вторую строку, в качестве направляющего столбца второй столбец, тогда направляющий элемент будет x₂ (коэффициент при нем равен a₂₂ ). Разделим направляющую строку на этот коэффициент и перепишем вновь полученную систему ограничений:

Далее умножаем направляющую строку поочередно на элементы, стоящие в направляющем столбце преобразуемого уравнения, и результат вычитаем из соответствующего уравнения. Иными словами, вначале умножаем направляющую строку на a₁₂ и вычтем полученный результат из первого уравнения. Далее направляющую строку умножим на a₃₂ и вычтем из третьего уравнения и т. д. до последнего m-го уравнения. Получим новую систему:

Матрицу, в которую преобразовалась расширенная матрица A_p после первого шага, обозначим A_p⁽¹⁾. В полученной матрице все элементы направляющего столбца, отличные от направляющего элемента, стали равными нулю. Совокупность элементов первых n столбцов матрицы A_p, лежащих вне направляющей строки и столбца предыдущего шага, называют главной частью матрицы A_p⁽¹⁾ данного преобразования. Направляющий элемент второго шага выбирают среди ненулевых элементов главной части матрицы A_p⁽¹⁾, матрицы полученной после проведенного преобразования.

Второй и дальнейший шаги метода проводят аналогично первому шагу. Последовательность действий продолжается до тех пор, пока имеется возможность выбора направляющего элемента. Если после k-го шага главная часть матрицы A_p^(k) не содержит ни одного элемента или содержит только нулевые элементы, то процесс исключения переменных заканчивается.

После проведения преобразований в системе может оказаться l уравнений, l m. Пусть это первые l по порядку уравнений, тогда система уравнений может быть записана в виде

(6)

Примем, что i-ой направляющей строке соответствует i-ый направляющий столбец, тогда ;

, j = 1,2,...,l

Следовательно, (6) можно записать в виде 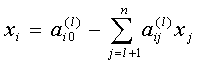 , причем переменные x_i являются базисными , а переменные x_s (s=l+1,n) - небазисными.