11. Алгоритм lu разложения матрицы.

LU-разложение (LU-метод, LU-факторизация) основан на том, что если главные миноры матрицы отличны от нуля, тогда матрицу можно представить, причем единственным образом, в виде произведения 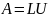(LU-декомпозиции), — нижняя треугольная матрица с ненулевыми диагональными элементами, — верхняя треугольная матрица с единичной диагональю.

Исходная матрица изменяется с помощью специальной матрицы преобразования .

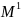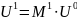
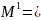
В результате этого преобразования элементы 1-го столбца ниже главной диагонали матрицы 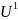будут равны 0. [Исключение 1-го неизвестного из всех уравнений, кроме 1.]

С помощью аналогичных преобразований получается матрица треугольного вида.

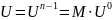
Из последнего равенства получается: , .

В результате разложения начальная система эквивалентна 2 системам:

Для определения вектора достаточно .

Вектор (решение исходной системы) определяется с помощью обратного хода Гаусса.

12. Решение систем линейных алгебраических уравнений с помощью lu разложения матрицы системы.

Пример решения СЛАУ с помощью LU-разложения.

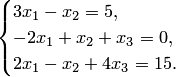
Факторизация:

: :

:

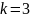Решение :

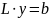Решение :

13. Алгоритм qr разложения матрицы.

Ортогональная матрица — квадратная с вещественными элементами, результат умножения которой на транспонированную равен единичной матрице.

QR-разложение — представление матрицы в виде произведения ортогональной и верхнетреугольной матрицы.

Метод состоит из крупных шагов. Каждый крупный шаг состоит из 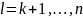мелких шагов. Исходная матрица изменяется на каждом мелком шаге с помощью специальной матрицы преобразования .

Для каждого : .

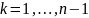и зависят от элементов на каждом шаге, удовлетворяют условию .

, .

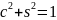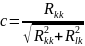За 1 мелкий шаг в матрице элемент с индексом будет равен 0. [Исключение k-го неизвестного из l-го уравнения системы.]

За 1 крупный шаг в матрице все элементы ниже главной диагонали в k-том столбце будут равны нулю. [Исключение k-того неизвестного из всех уравнений кроме k-того.]

В итоге получается матрица треугольного вида.

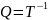
В результате разложения начальная система эквивалентна 2 системам:

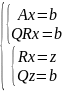
Для определения вектора достаточно .

Вектор (решение исходной системы) определяется с помощью обратного хода Гаусса.

15. Использование lu и qr разложения матрицы системы для решения систем с одинаковой матрицей и различными правыми частями (на примере вычисления обратных матриц).

Использование LU-разложения для вычисления обратной матрицы.

— неизвестные векторы, столбцы обратной матрицы.

Т. к. , векторы удовлетворяют равенствам:

, , …, .

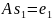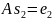Задача нахождения обратной матрицы сведена к задаче решения систем с одной матрицей и различными правыми частями. При решении этих систем LU-разложение матрицы необходимо выполнить только 1 раз.

Вычисление обратной матрицы с помощью QR — аналогично LU.