II. Численные методы линейной алгебры.

8. Нормы векторов и матриц. Относительная и абсолютная погрешность вектора. Связь погрешности решения систем линейных алгебраических уравнений и невязки.

Норма — число, отличное от нуля. Предназначена для сравнения векторов, матриц, и т. п. (какой вектор/матрица «больше», какой «меньше»).

Нормы векторов.

Норма вектора — число, характеризующее величину многомерного объекта.

Норма вектора — число, обозначаемое и удовлетворяющее следующим условиям — аксиомам нормы (обобщающим свойства длины 3-мерного в-ра):

1. , причем .

2. , — действительное число.

3. — неравенство треугольника.

Часто норму обозначают в виде .

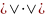Нормированное пространство — векторное пространство с нормой, аксиомы нормы в таком случае — аксиомы нормированного пространства.

Нормированный вектор (нормальный) — с единичной нормой ( ).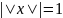

Любой ненулевой вектор можно нормировать, т. е. разделить его на свою норму: вектор имеет единичную норму. С геометрической точки зрения это значит, что мы берем сонаправленный вектор единичной длины.

Векторные нормы в различных пространствах: см. вопрос 3.

Абсолютная погрешность вектора: .

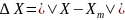Относительная погрешность вектора: .

Нормы матриц.

Норма матрицы A — вещественное число , удовлетворяющее условиям:

1. 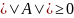, причем .

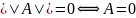2. , — действительное число.

3. — неравенство треугольника.

Виды матричных норм:

• Если выполняется 4-ое условие: 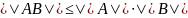, норма называется мультипликативной.

• Операторная норма, порожденная векторной нормой — число .

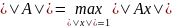• Матричная норма, составленная как операторная, называется подчинённой по отношению к норме, использованной в пространствах векторов.

• m-норма: .

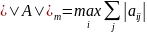• l-норма: .

• Норма Фробениуса:

Невязка — вектор . — система уравнений.

Связь между погрешностью решения СЛАУ и величиной невязки определяется числом обусловленности матрицы — характеристикой, не связанной с каким-либо численным алгоритмом и отражающей только свойства системы. Это число обозначают Cond(A) и определяют по формуле: .

9. Характеристика и отличительные особенности прямых и итерационных методов численного решения систем линейных алгебраических уравнений. Примеры.

Численное решение уравнений и их систем — приближённое определение корней уравнения или системы уравнений. Применяется, когда точное значение вычислить невозможно или очень трудоёмко.

Методы численного решения СЛАУ делятся на прямые и итерационные.

Прямые методы — позволяющие получить решение системы за конечное число арифметических операций. Метод Крамера, метод Гаусса, LU-метод и т.д.

Итерационные методы (методы последовательных приближений) — решение системы находится как предел последовательных приближений при номере итерации . При использовании методов итерации обычно задается некоторое малое число и вычисления проводятся до тех пор, пока не будет выполнена оценка . Метод Зейделя, Якоби, метод верхних релаксаций и т.д.

Реализация прямых методов на компьютере приводит к решению с погрешностью, т. к. все арифметические операции над переменными с плавающей точкой выполняются с округлением. В зависимости от свойств матрицы исходной системы эти погрешности могут достигать значительных величин.

1. Метод Жордана-Гаусса (метод последовательного исключения неизвестных).

Алгоритм. Система в развернутом виде:

Метод Гаусса состоит в последовательном исключении неизвестных из этой системы. Предположим, что . исключается из всех уравнений, кроме первого, последовательно умножая первое уравнение на и складывая с i-м уравнением:

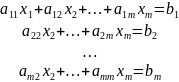
Прямой ход Гаусса. Аналогичным образом исключаются остальные неизвестные и получается система треугольного вида:

Можно получить все значения неизвестных, выполняя последовательные подстановки в последней системе (начиная с последнего уравнения). Обратный ход Гаусса.

Характеристики. Метод легко реализуем на компьютере. При выполнении вычислений, как правило, не интересуют промежуточные значения матрицы . Поэтому численная реализация метода сводится к преобразованию элементов массива размерности , где столбец содержит элементы правой части системы.

Один из основных недостатков: накапливается вычислительная погрешность.

2. LU-метод — см. вопросы 11-12.

3. QR-метод — см. вопросы 13-14.