6. Обусловленность вычислительной задачи и вычислительного алгоритма. Абсолютное и относительное число обусловленности.

Корректность задач

Корректная вычислительная задача — если:

1. Её решение существует при любых входных данных.

2. Решение единственно.

3. Решение устойчиво по отношению к малым возмущениям входных данных.

Решение устойчиво по входным данным вычислительной задачи , если оно зависит от входных данных непрерывным образом:

Относительная устойчивость: вместо и 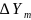ставятся и .

Обусловленность вычислительной задачи — чувствительность её решения к малым погрешностям входных данных.

Число обусловленности — количественная мера степени обусловленности вычислительной задачи.

, коэффициент — абсолютное число обусловленности.

, коэффициент — относительное число обусловленности.

Плохо обусловлена: при .

Корректность алгоритмов

Вычислительный алгоритм — точное предписание действий над входными данными, задающее вычислительный процесс, направленный на преобразование произвольных входных данных в полностью определенный этими входными данными результат.

Корректный вычислительный алгоритм — если:

1. После выполнения конечного числа элементарных операций любые входные данные можно преобразовать в результат.

2. Результат устойчив по отношению к малым возмущениям входных данных. Устойчивость по входным данным означает, что результат непрерывным образом зависит от входных данных при условии, что отсутствует вычислительная погрешность.

3. Результат обладает вычислительной устойчивостью.

Вычислительно устойчивый алгоритм — если вычислительная погрешность результата стремится к нулю при стремящейся к нулю машинной погрешности .

Устойчивый алгоритм — устойчивый по входным данным и вычислительно устойчивый.

Хорошо обусловленный вычислительный алгоритм — если малые относительные погрешности округления (характеризуемые ) приводят к малой относительной вычислительной погрешности результата .

, — число обусловленности алгоритма.

Плохо обусловленный алгоритм — если .

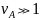7. Понятие оператора и неподвижной точки оператора. Принцип сжимающих отображений.

Сжимающее отображение — отображение метрического пространства в себя, уменьшающее расстояние между любыми двумя точками не менее чем в 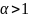раз.

«Принцип сжимающих отображений». Согласно теореме Банаха, у сжимающего отображения полного метрического пространства в себя существует неподвижная точка, причём ровно одна. Принцип широко используется при доказательстве различных математических утверждений.

Пусть на метрическом пространстве определён оператор . Он называется сжимающим на , если существует такое неотрицательное число , что для любых двух точек выполняется неравенство .

Неподвижная точка отображения — точка, которую отображение переводит в неё же, иными словами, решение уравнения .

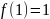#: отображение имеет неподвижные точки и , т. к. и .

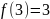Отображение с тремя неподвижными точками:

Периодическая тока — возвращающаяся в себя после определённого числа итераций, то есть, решение уравнения (в частности, неподвижная — это периодическая точка периода 1).

Свойства.

Непрерывность. — метрическое пространство, — сжимающий оператор на . Тогда — непрерывная функция на .

Неподвижная точка. По теореме Банаха у сжимающего отображения существует единственная неподвижная точка .