3. Линейные нормированные пространства. Аксиомы нормы. Примеры определения норм в различных пространствах.

Множество становится пространством, когда в нем вводятся отношения (отношение порядка, расстояния).

Линейное пространство — частный случай метрического. В нем определены операции сложения и умножения на число.

Норма вектора — число, обозначаемое и удовлетворяющее следующим условиям — аксиомам нормы (обобщающим свойства длины 3-мерного в-ра):

1. , причем .

2. , 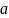— действительное число.

3. — неравенство треугольника.

Подробнее о нормах: см. вопрос 8.

Нормированное пространство — векторное пространство с нормой, аксиомы нормы в таком случае — аксиомы нормированного пространства.

Линейное нормированное пространство — в котором задана норма.

Всякое нормированное — метрическое, не всякое линейное — нормированное.

Примеры определения норм в различных пространствах.

Норма в линейном пространстве — расстояние от 0 до элемента.

Евклидово пространство — конечномерное вещественное векторное пространство с введённым на нём скалярным произведением, порождающим норму:

Норма в евклидовом пространстве: 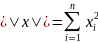— евклидова/сферическая норма (простейший случай). Когда говорят о евклидовой норме, не уточняя, обычно имеют в виду сферическую.

Норма в линейном арифметическом пространстве : функция вида

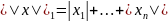— октаэдрическая норма (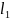 -норма).

Функция , заданная на векторах в — кубическая норма (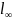 -норма).

Единичная сфера — множество векторов нормированного пространства, удовлетворяющих условию (единичных векторов). Зависит от линейного пространства и однозначно определяет рассматриваемую в нем форму.

На рис. 1 изображен вид единичной сферы для различных норм 2-мерного лин. пространства: сферической, октаэдрической, кубической.

На рис. 2 изображены единичные сферы указанных норм в 3-мерном лин. пространстве.

Вид единичной сферы для этих норм послужил источником для их названий.

4. Элементы общей теории погрешностей. Основные определения, утверждения (абсолютная и относительная погрешности, погрешности основных арифметических операций).

Численное решение любой задачи, как правило, осуществляется приближенно, с различной точностью. Это может быть обусловлено неточностью исходных данных, разрядностью вычислений и т. п.

Главная задача численных методов — фактическое нахождение решения с требуемой или, по крайней мере, оцениваемой точностью.

Погрешность измерения — оценка отклонения приближенного/измеренного значения величины от её истинного значения. Полная погрешность вычислений состоит из двух составляющих: 1) неустранимая погрешность; 2) устранимая погрешность.

Неустранимая погрешность обусловлена неточностью исходных данных и никаким образом не может быть уменьшена в процессе вычислений.

Устранимая погрешность состоит из двух составляющих: а) погрешность метода/аппроксимации; б) погрешность вычислений. Эти составляющие могут быть уменьшены выбором более точных методов и увеличением разрядности вычислений.

Абсолютная погрешность — модуль разности между истинным значением величины и её измеренным значением.

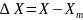
Относительная погрешность — отношение абсолютной погрешности к модулю измеренного значения величины.

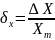
[Индекс — от слова measured (измеренный).]

Погрешности основных математических операций.

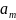, — приближенные значения чисел и .

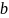1. Абсолютная, сумма и разность. Абсолютная погрешность алгебраической суммы или разности не превосходит суммы абсолютных погрешностей слагаемых, т. е.:

2. Относительная, сумма и разность. , — ненулевые приближенные значения одного знака.

• , . При суммировании чисел одного знака не происходит потери точности (если оценивать относительную точность).

• , . При вычитании чисел одного знака относительная погрешность возрастает в раз.

3. Относительная, произведение и частное.

• .

• , .