VII. Приближение функций и смежные вопросы.

64. Формулировка задачи приближения функций. Равномерные и среднеквадратичные приближения. Понятие об элементах наилучшего приближения.

65. Формулировка задачи среднеквадратичного приближения. Метод наименьших квадратов.

66. Применение метода наименьших квадратов для получения эмпирических зависимостей (на примере способа «выравнивания данных»).

67. Кривые Безье. Определение. Способы построения кривых Безье 2 и 3 порядка.

68. Преобразование Фурье. Непрерывное и дискретное преобразование Фурье.

69. Понятие о быстром преобразовании Фурье. Примеры использования преобразования Фурье в прикладных исследованиях.

    1. Основные понятия.

1. Понятие метрики и метрического пространства, примеры.

Метрическое пространство — множество, в котором определено расстояние между любой парой элементов.

Метрика (расстояние, функция расстояния) — числовая функция 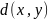(на множестве 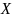, точки 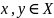), которая удовлетворяет следующим аксиомам (аксиомам расстояния):

1. (аксиома тождества).

2. 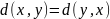(аксиома симметрии).

3. (аксиома треугольника, неравенство треугольника).

Метрическое пространство — совокупность/пара . — некоторое множество (подлежащее множество метрического пространства, множество точек метрического пространства). — метрика; принимает значения в множестве вещественных чисел.

Обозначения.

Обычно расстояние между точками и в метрическом пространстве 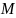обозначается или .

• В метрической геометрии принято обозначение или 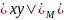, если необходимо подчеркнуть, что речь идет о . Реже употребляются обозначения и .

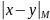• В классической геометрии приняты обозначения или (точки обычно обозначают заглавными латинскими буквами).

Примеры:

• Пространство изолированных точек. Для произвольного множествах X ф-ия расстояния: , если . 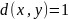во всех остальных случаях. Дискретная метрика.

• Пространство действительных чисел. Метрика: 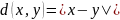. Такое пространство называется полным метрическим.

• Пространство векторов с вещественными координатами 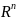. Метрика: .

• Пространство 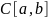непрерывных на отрезке функций. Метрика: .

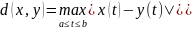Полное пространство — метрическое пространство, в котором каждая фундаментальная последовательность сходится (к элементу этого же пространства).

2. Сходящиеся и фундаментальные последовательности, открытые и замкнутые шары, полные метрические пространства.

Сходящаяся последовательность (сходится к ) — если . Т. е. если для всякого найдется такое число , что для всех имеет место .

Фундаментальная последовательность (сходящаяся в себе последовательность, последовательность Коши) — последовательность точек метрического пространства такая, что для любого заданного расстояния существует элемент последовательности, начиная с которого все элементы последовательности находятся друг от друга на расстоянии менее, чем заданное. .

Открытый шар 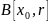в метрическом пространстве — совокупность точек , удовлетворяющих условию .

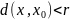Замкнутый шар в метрическом пространстве — совокупность точек , удовлетворяющих условию .

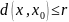— центр шара, — радиус шара.

Пространство полное, если в метрическом пространстве каждая фундаментальная последовательность имеет предел.