35. Вычислительная схема Эйткена.

Схема Эйткена предлагает более удобную форму нахождения полинома Лагранжа.

На первом этапе вычисляются многочлены , построенные на каждой паре соседних узлов 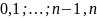соответственно.

Многочлены, построенные на паре соседних узлов:

.

Затем на основе них вычисляются построенные на тройках соседних узлов:

.

И т.д. пока не получится один многочлен, построенный на всех узлах интерполяции:

Полученный многочлен .

36. Оценка погрешности интерполяции многочленом Лагранжа.

. Многочлен построен так, что .

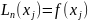Вычисляя погрешность 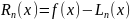, можно получить следующую формулу для оценки погрешности интерполяционной формулы Лагранжа:

.

Такая оценка возможна только когда известно аналитическое выражение для . Если задана таблично, то производные заменяются конечными разностями.

37. Разделенные разности, основные свойства. Интерполяционный многочлен Ньютона, особенности применения, оценка погрешности.

Интерполяционные формулы Ньютона.

Первая интерполяционная формула Ньютона.

Пусть , , .

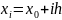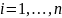Нужно построить , удовлетворяющий 2 условиям:

1. Степень полинома не должна превышать .

2. .

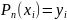Формула для первой интерполяционной формулы Ньютона имеет вид:

,

где .

Первая формула применяется когда находится в начале таблицы. Тогда в качестве следует брать ближайшее слева к заданному табличное значение.

Вторая интерполяционная формула Ньютона.

Когда значение аргумента находится ближе к концу отрезка интерполяции, применять первую формулу становится невыгодно. Поэтому применяется вторая интерполяционная формула Ньютона.

где .

Здесь в качестве следует брать ближайшее справа к заданному табличное значение.

40. Определение сплайна. Гладкая кусочно-полиномиальная интерполяция. Определение интерполяционного сплайна.

Сплайн — функция, область определения которой разбита на конечное число отрезков, на каждом из которых сплайн совпадает с некоторым алгебраическим полиномом. Максимальная степень из использованных полиномов называется степенью сплайна. Разность между степенью сплайна и получившейся гладкостью называется дефектом сплайна.

Кусочно-полиномиальная интерполяция. Для снижения погрешностей отрезок разбивается на частичные отрезки и на каждом из них функцию заменяют приближенно полиномом невысокой степени.

Интерполяционный сплайн — совпадающий с данной функцией в заданных различных точках.

Сплайн, соответствующий данной функции и узлам интерполяции — функция 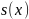, удовлетворяющая условиям:

1. На каждом отрезке функция является кубическим многочленом.

2. Функция, ее первая и вторая производные непрерывны на отрезке [a,b].

3. . Условие интерполирования.

Интерполяционный кубический сплайн — удовлетворяющий условиям 1-3. Наиболее распространен.

42. Глобальные и локальные кубические интерполяционные сплайны, Определения и способы построения.

Кубический сплайн — функция , удовлетворяющая 3 условиям:

1. На каждом отрезке функция является кубическим многочленом.

2. Функция, ее первая и вторая производные непрерывны на отрезке [a,b].

3. . Условие интерполирования.