IV. Интерполирование функций.
32. Задача интерполяции. Обобщенный многочлен по системе функций. Глобальная и локальная интерполяции. Преимущества и недостатки. Примеры.
Аппроксимация. Зачем нужна, примеры.
Аппроксимация — метод, состоящий в замене объектов другими объектами, близкими к исходным, но более простыми. Позволяет исследовать числовые характеристики и качественные свойства объекта, сводя задачу к изучению более простых или более удобных объектов (#, характеристики которых легко вычисляются, или свойства которых уже известны). В геометрии рассматриваются аппроксимации кривых ломаными. Некоторые разделы математики целиком посвящены аппроксимации (#, теория приближения функций, численные методы анализа).
Аппроксимация
функций — приближенная замена
заданной функции другой функцией так,
чтобы их отклонение друг от друга в
заданной области было минимальным.
Аппроксимирующая функция —
заменяющая; обозначается
.
Исходная обозначается
.
Типичной задачей аппроксимации является
задача интерполяции.
Пусть в пространстве
заданы точки
,
имеющие в некоторой системе координат
имеют радиус-векторы
.
Задача интерполяции состоит в построении кривой, проходящей через указанные точки в указанном порядке. Узлы интерполяции — точки, через которые проходит кривая.
Обобщенный
многочлен по системе функций: линейные
комбинации
.
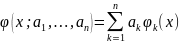Локальная интерполяция — если таблица значений используется по частям. Глобальная — наоборот.
33. Интерполяция алгебраическими многочленами. Системы функций Чебышёва. Существование и единственность интерполяционного алгебраического многочлена.
Интерполяция
алгебраическими многочленами функции
на отрезке
— построение многочлена
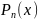степени
,
принимающего в узлах интерполяции
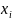значения
:
,
.
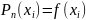После выбора вида интерполяции задача сводится к вычислению коэффициентов обобщенного многочлена. Если определитель отличен от 0, можно решать.
Система функций
Чебышёва — система ЛН функций, у
которой определитель
для любого набора узлов.
Система уравнений, определяющих коэффициенты многочлена, имеет вид:
.
Её определителем является определитель Вандермонда:
Существование
и единственность интерполяционного
многочлена гарантируется, если все
узлы интерполяции
различны. Определитель СЛАУ для
нахождения коэффициентов
является определителем Вандермонда,
отличном от нуля, когда все узлы
различны. Поскольку матрица системы
невырождена (определитель
),
то решение системы существует и
единственно. Т. е. интерполяционный
полином существует и единственный.
34. Интерполяционный многочлен Лагранжа, особенности применения.
Интерполяционный
многочлен Лагранжа. Для
пар чисел
,
где все
различны, существует единственный
многочлен
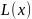степени не более
,
для которого
.
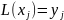В простейшем
случае: при
линейный многочлен, график которого —
прямая, проходящая через 2 заданные
точки.
Вычисление.
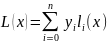
где базисные полиномы определяются по формуле:
обладают следующими
свойствами:
Являются многочленами степени .
,
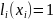
Отсюда следует,
что
— как линейная комбинация
— может иметь степень не больше
,
и
.
Применение многочлена Лагранжа:
Конечная коммутативная группа матриц над полем
приводится к диагональному виду (поле
должно содержать все корни k-ой степени
из единицы, где
— порядок группы, и чтобы
не делилось на характеристику поля
).Алгебраическое уравнение степени <5 решается в радикалах.
Линейное дифференциальное уравнение с постоянными коэффициентами решается в явном виде.
Для любого полинома от одной переменной с рациональными коэффициентами явно решается следующая задача: определить, раскладывается ли полином на множители, являющиеся полиномами положительных степеней с рациональными коэффициентами; если «да», то найти его разложение на множители.