Критерий Фридмана
Критерий применяется для сопоставления показателей, измеренных в c условиях (c≥3) на одной и той же выборке из n испытуемых. Критерий Фридмана позволяет установить, что величины показателей от условия к условию изменяются, но при этом не указывает на направление изменений и в этом смысле похож на критерий знаков.
Критерий Фридмана является обобщением критерия Вилкоксона на большее, чем два, количество условий измерения, в котором мы ранжируем не абсолютные величины сдвигов, а сами индивидуальные значения измерений.
Нулевая гипотеза H0={между полученными в разных условиях показателями существуют лишь случайные различия}.
Рассмотрим использование критерия Фридмана на примере. Пять учащихся исследуются по четырём тестам. Являются ли результаты тестирования случайными?
|
Оценки в баллах по проведённым тестам |
|||
Номер испытуемого |
Тест A |
Тест B |
Тест C |
Тест D |
1 |
3.6 |
4.1 |
2.9 |
3.5 |
2 |
3.8 |
4.2 |
3.7 |
4.6 |
3 |
3.3 |
3.8 |
3 |
3.7 |
4 |
3.8 |
3.3 |
3.4 |
2.7 |
5 |
4 |
3.6 |
1.9 |
3.1 |
Проранжируем индивидуальные значения показателей для каждого испытуемого в порядке убывания признака. Т.е. производим ранжирование параметров каждой строки представленной таблицы.
Найдём суммы рангов по столбцам. В результате получаем:
|
Ранги тестов (по строкам) |
|||
Номер испытуемого |
Тест A |
Тест B |
Тест C |
Тест D |
1 |
2 |
1 |
4 |
3 |
2 |
3 |
2 |
4 |
1 |
3 |
3 |
1 |
4 |
2 |
4 |
1 |
3 |
2 |
4 |
5 |
1 |
2 |
4 |
3 |
Сумма рангов: |
10 |
9 |
18 |
13 |
Найдём
эмпирическое значение критерия по
формуле:
где c
– количество условий (тестов, т.е. c=4),
n
– количество испытуемых (n=5),
Tj
– сумма рангов по j-ому
условию (тесту).
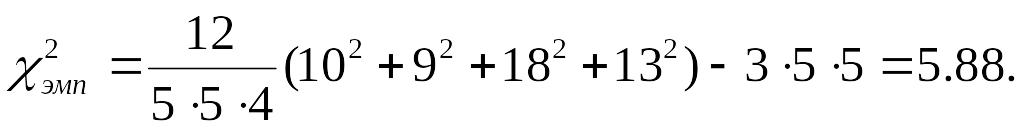
Найдём
по таблице критическое значение критерия
,
зависящее от уровня значимости α и
степени свободы k=c-1.
В нашем случае k=4-1=3 и возьмем α=0,05
получим:
Проверим,
можно ли на данном уровне значимости
принять нулевую гипотезу, утверждающую
о несущественности различий результатов
тестов. Нулевая гипотеза принимается,
если критическое значение превосходит
эмпирическое.
Вывод: нулевая гипотеза принимается, т.е. результаты теста можно считать случайными (различия несущественны).
Схема применения критерия имеет вид:
Записать значения признаков для каждого из n испытуемых |
Найти сумму Tj рангов для каждого признака
|
Н 0 принимается, если |
Н айти
|
Найти критическое значение критерия по таблице
|
Проранжировать индивидуальные значения c показателей для каждого испытуемого |
Следующий критерий можно рассматривать как продолжение критерия Фридмана, поскольку он не только констатирует различия, но и указывает на направление изменений.